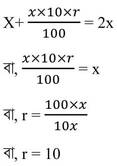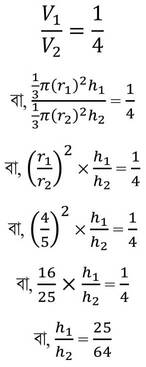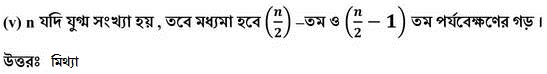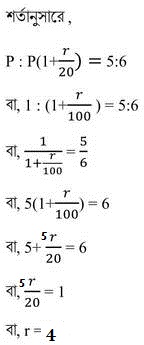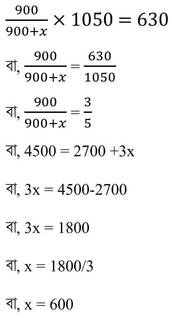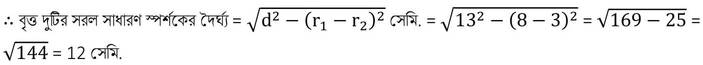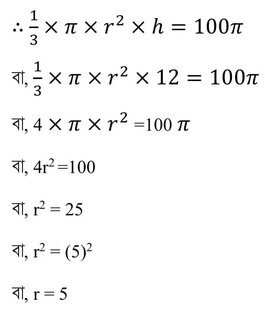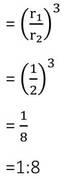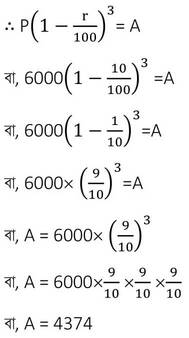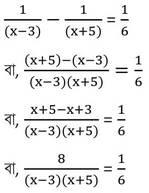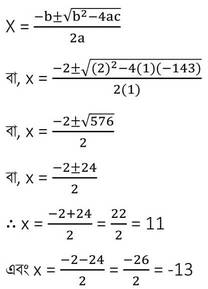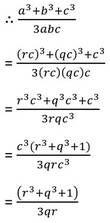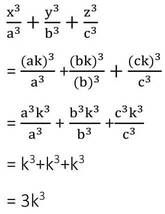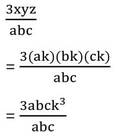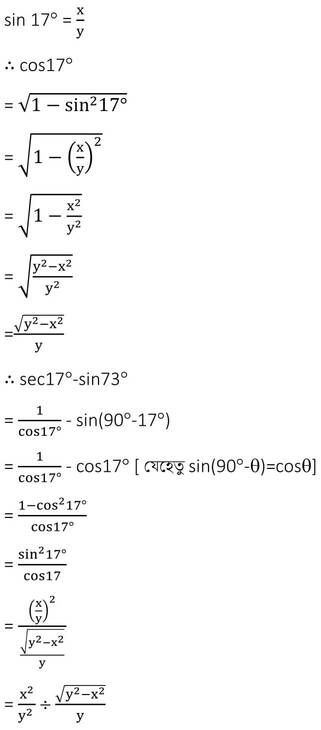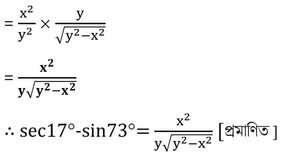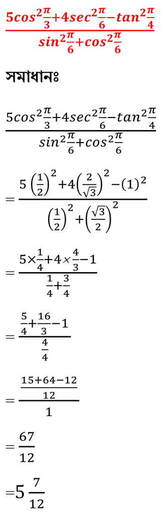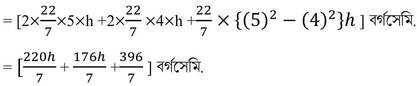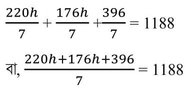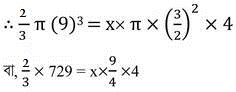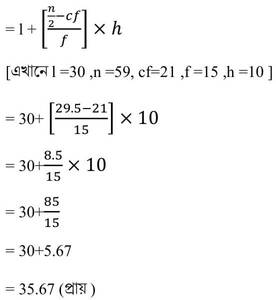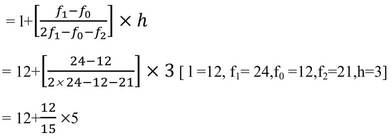Madhyamik 2020 Math Question Solution.
মাধ্যমিক ২০২০ গণিত প্রশ্ন উত্তর |মাধ্যমিক ২০২০ অঙ্ক প্রশ্নের সমাধান
Madhyamik 2020 Math Question Solution|মাধ্যমিক ২০২০ গণিত সমাধান
1. নিম্নলিখিত প্রশ্নগুলির প্রতিটি ক্ষেত্রে সঠিক উত্তর নির্বাচন করঃ
(i) কোনো মূলধন 10 বছরে দ্বিগুন হলে , বার্ষিক সরল সুদের হার –
(a) 5%
(b) 10%
(c ) 15%
(d) 20%
Ans:
সমাধানঃ ধরি , মূলধনের পরিমাণ x টাকা এবং বার্ষিক সরল সুদের হার r%
শর্তানুসারে ,
∴ বার্ষিক সরল সুদের হার 10%
(ii) x2-7x+3=0 সমীকরণের বীজদ্বয়ের গুনফল
(a) 7
(ii) -7
(c ) 3
(d) -3
Ans: (c ) 3
সমাধানঃ x2-7x+3=0 সমীকরণের বীজদ্বয়ের গুনফল
(iii) O কেন্দ্রীয় বৃত্তের AB ও CD জ্যা দুটির দৈর্ঘ্য সমান , ∠AOB = 60° হলে, ∠COD এর মান কত হবে-
(a) 30°
(b) 60°
(c ) 120°
(d) 180°
Ans: (b) 60°
সমাধানঃ আমরা জানি সমান জ্যা বৃত্তের কেন্দ্রে সমান কোণ উৎপন্ন করে ।
∴ ∠AOB=∠COD =60°
(iv) দুটি লম্ব বৃত্তাকার শঙ্কুর আয়তনের অনুপাত 1:4 এবং তাদের ভূমিতলের ব্যাসার্ধের দৈর্ঘ্যের অনুপাত 4:5 হলে তাদের উচ্চতার অনুপাত-
(a) 1:5
(b) 5:4
(c ) 25:16
(d) 25:64
Ans: (d ) 25:64
সমাধানঃ ধরি , শঙ্কু দুটির ভূমিতলের ব্যাসার্ধ যথাক্রমে r1 একক এবং r2 একক এবং শঙ্কু দুটির উচ্চতা যথাক্রমে h1 একক এবং h2 একক এবং শঙ্কু দুটির আয়তন যথাক্রমে V1ঘন একক ও V2 ঘন একক
∴ r1:r2 = 4:5
এবং , V1: V2 = 1:4
∴ h1:h2 = 25:64
(v) যদি , sinϴ-cosϴ=0 ,(0° ≤ ϴ≤ 90°) এবং secϴ+cosecϴ =x ,হয় তাহলে x এর মান –
(a) 1
(b) 2
(c ) √2
(d) 2√2
Ans: (d) 2√2
সমাধানঃ
sinϴ -cosϴ= 0
বা, sinϴ = cosϴ
বা, tanϴ = 1
বা, tanϴ =tan45°
বা, ϴ=45°
∴ secϴ +cosecϴ =x
বা, sec 45° +cosec 45° =x
বা, √2 + √2 =x
বা, 2√2 = x [উত্তর]
(vi) 1,3,2,8,10,8,3,2,8,8 এর সংখ্যাগুরু মান –
(a) 2
(b) 3
(c ) 8
(d) 10
Ans: (c ) 8
2. শূন্যস্থান পূরণ করঃ
(i) আনিসূর 500 টাকা 9 মাসের জন্য এবং ডেভিড 600 টাকা 5 মাসের জন্য একটি যৌথ ব্যাবসা শুরু করে । তাদের লভ্যাংশের অনুপাত হবে __________ ।
উত্তরঃ 3:2
সমাধানঃ আনিসূর 500 টাকা 9 মাসের জন্য এবং ডেভিড 600 টাকা 5 মাসের জন্য একটি যৌথ ব্যাবসা শুরু করে । তাদের লভ্যাংশের অনুপাত = তাদের মূলধনের অনুপাত = (500✕9) : (600✕5) = 4500:3000 = 3:2
(ii) ax2+2bx+c=0 (a≠0) ,দ্বিঘাত সমীকরণের বীজদ্বয় বাস্তব ও সমান হলে b2 =________ হবে ।
Ans: 4ac
(iii) দুটি কোণের সমষ্টি ________ হলে তাদেরকে পরস্পরের সম্পূরক বলা হয় ।
Ans: 180°
(iv) sin3ϴ এর সর্বচ্চ মান __________ ।
Ans: 1
(v) একটি নিরেট গোলক গলিয়ে একটি নিরেট লম্ব বৃত্তাকার চোঙ তৈরি করা হলে গোলক ও চোঙের ________ সমান হবে ।
Ans: আয়তন
(vi) কিছু ছাত্রের বয়স হলো (বছরে ) 10,11,9,7,13,8,14 এদের বয়সের মধ্যমা হল _____________ বছর ।
Ans:
সমাধানঃ কিছু ছাত্রের বয়স হলো (বছরে ) 10,11,9,7,13,8,14
মানের ঊর্ধ্বক্রমে সাজিয়ে পাই ,
7,8,9,10,11,13,14
এক্ষেত্রে n = 7(বিজোড় সংখ্যা )
∴ মধ্যমা = (n+1)/2 তম মান = (7+1)/2 তম মান = 4 তম মান =10 বছর
3. সত্য বা মিথ্যা লেখঃ
(ii) 2a =3b=4c হলে a:b:c =2:3:4
উত্তরঃ মিথ্যা
সমাধানঃ
a:b:c = 6:4:3
(iii) একটি ত্রিভুজের তিনটি বাহুর দৈর্ঘ্যের অনুপাত 5:12:13 হলে ত্রিভুজটি সমকোণী ত্রিভুজ হবে ।
উত্তরঃ সত্য ।
ধরি , ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য যথাক্রমে 5k একক ,12k একক এবং 13k একক ।
এখন , (13k)2 =169k2 = 144k2 +25k2 = (12k)2 +(5k)2
∴ (13k)2 =(12k)2 +(5k)2
∴ ত্রিভুজটি সমকোণী ত্রিভুজ ।
(iv) একটি রশ্মির প্রান্তবিন্দুকে কেন্দ্র করে , রশ্মিটিকে ঘড়ির কাঁটার বিপরীত দিকে ঘোরার জন্য উৎপন্ন কোণটি ধনাত্মক হবে ।
উত্তরঃ সত্য
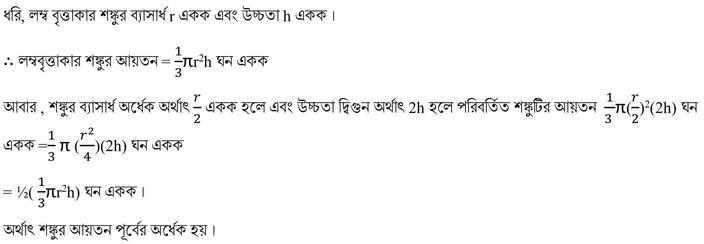
(vi) একটি লম্ব বৃত্তাকার শঙ্কুর ভূমিতলের ব্যাসার্ধের দৈর্ঘ্য অর্ধেক এবং উচ্চতা দ্বিগুন করা হলে শঙ্কুর আয়তন একই থাকে ।
উত্তরঃ মিথ্যা ।
ধরি, লম্ব বৃত্তাকার শঙ্কুর ব্যাসার্ধ r একক এবং উচ্চতা h একক ।
4.
(i) কোনো আসল ও তার 5 বছরের সবৃদ্ধি মূলের অনুপাত 5:6 হলে , বার্ষিক সরল সুদের হার নির্ণয় কর ।
সমাধানঃ ধরি , আসলের পরিমাণ P টাকা এবং বার্ষিক সরল সুদের হার r%
∴ বার্ষিক সরল সুদের হার 4%
(ii) A ও B কোনো ব্যাবসায় 1050 টাকা লাভ করে । A এর মূলধন 900 টাকা এবং লভ্যাংশ 630 টাকা হলে B এর মূলধন কত ?
সমাধানঃ ধরি , B এর মূলধন x টাকা ।
∴ A ও B এর মূলধনের অনুপাত 900:x
শর্তানুসারে ,
∴ B এর মূলধন 600 টাকা ।
(iii) x ∝ y, y ∝ z এবং z ∝ x হলে, ভেদ ধ্রুবক তিনটির গুনফল নির্ণয় কর ।
সমাধানঃ x ∝ y
∴ x = k1y [ k1 একটি অশূন্য ভেদ ধ্রুবক ]—-(i)
এবং , y ∝ z
∴ y = k2z [k2 একটি অশূন্য ভেদ ধ্রুবক ]—-(ii)
আবার , z ∝ x
∴ z = k3x [ k3 একটি অশূন্য ভেদ ধ্রুবক ]—-(iii)
(i),(ii) ও (iii) নং সমীকরণকে গুন করে পাই ,
xyz = k1k2k3xyz
বা, k1k2k3 = xyz/xyz
বা, k1k2k3 = 1
∴ ভেদ ধ্রুবক তিনটির গুণফল 1 [ এটাই ভেদধ্রুবক তিনটির মধ্যে সম্পর্ক ]
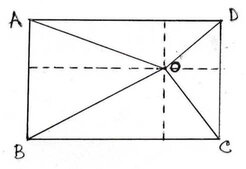
(iv) ABCD আয়তকার চিত্রের অভ্যন্তরে O বিন্দু এমনভাবে অবস্থিত যে OB=6সেমি., OD= 8 সেমি. এবং OA=5 সেমি. । OC এর দৈর্ঘ্য নির্ণয় কর ।
সমাধানঃ
ABCD আয়তকার চিত্রের অভ্যন্তরে O একটি বিন্দু হলে , OA2+OC2 = OB2+OD2হয় ।
∴ OA2+OC2 = OB2+OD2
বা, (5)2+OC2 = (6)2+(8)2
বা, 25+OC2 = 36+64
বা, OC2 = 100-25
বা, OC2 = 75
বা, OC2 = (5√3)2
বা, OC = 5√3
∴ OC এর দৈর্ঘ্য 5√3 সেমি. ।
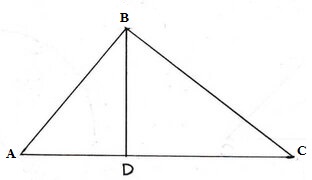
(vi) ABC একটি সমকোণী ত্রিভুজের ∠ABC =90° AB=3সেমি. এবং BC=4 সেমি. এবং B বিন্দু থেকে AC বাহুর উপর লম্ব BD যা AC বাহুর সঙ্গে D বিন্দুতে মিলিত হয় । BD এর দৈর্ঘ্য নির্ণয় কর ।
সমাধানঃ
ABC ত্রিভুজের ∠ABC = 90° এবং সমকৌণিক বিন্দু B থেকে অতিভুজ AC এর উপর BD লম্ব । । যেহেতু সমকোণী ত্রিভুজের সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অঙ্কন করলে লম্বের উভয়পার্শ্বে যে দুটি ত্রিভুজ উৎপন্ন হয় তারা পরস্পর সদৃশ ।
∴ ∆BDC এবং ∆ADB পরস্পর সদৃশ ।
∴ BD এর দৈর্ঘ্য 2 পূর্ণ 2/5 সেমি. ।
(vii) দুটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 8সেমি. ও 3 সেমি. । তাদের কেন্দ্র দ্বয়ের মধ্যে দূরত্ব 13 সেমি. । বৃত্ত দুটির সরল সাধারণ স্পর্শকের দৈর্ঘ্য নির্ণয় কর ।
সমাধানঃ দুটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 8সেমি. ও 3 সেমি. । তাদের কেন্দ্র দ্বয়ের মধ্যে দূরত্ব 13 সেমি.
∴ r1 = 8 সেমি. এবং r2 = 3সেমি. এবং d =13সেমি.
(viii) একটি ঘড়ির ঘণ্টার কাঁটা 1 ঘণ্টায় যে কোণ আবর্তন করে তার বৃত্তীয় মান নির্ণয় কর ।
সমাধানঃ একটি ঘড়ির ঘণ্টার কাঁটা 12 ঘণ্টায় আবর্তন করে 360°
যেহেতু ঘড়ির কাঁটা ঘুরলে ঋণাত্মক কোণ উৎপন্ন করে
1 ঘণ্টায় ঘড়ির ঘণ্টার কাঁটা যে কোণ উৎপন্ন করে তার বৃত্তীয় মান -π /6
(ix) tan4ϴ tan6ϴ =1 এবং 6ϴ ধনাত্মক সূক্ষ্মকোণ হলে , ϴ -এর মান নির্ণয় কর ।
সমাধানঃ
tan4ϴ tan6ϴ = 1
বা, tan4ϴ = 1/ tan6ϴ
বা, tan4ϴ = cot6ϴ
বা, tan4ϴ = tan(90°-6ϴ )
বা, 4ϴ =90°-6ϴ
বা, 10ϴ =90°
বা, ϴ = 90°/10 = 9°
∴ ϴ =9°
(x) কোনো লম্ব বৃত্তাকার শঙ্কুর উচ্চতা 12 সেমি এবং আয়তন 100π ঘন সেমি.। শঙ্কুর তির্যক উচ্চতা নির্ণয় কর ।
সমাধানঃ ধরি , শঙ্কুর ভূমিতলের ব্যাসার্ধ r সেমি.
শঙ্কুর উচ্চতা (h ) = 12 সেমি.
শঙ্কুর আয়তন = 100 π ঘন সেমি.
ধরি, শঙ্কুর ব্যাসার্ধ r সেমি.
শঙ্কুর তির্যক উচ্চতা l হলে ,
l2=h2+r2
বা, l2 = (12)2+(5)2
বা, l2 = 144+25
বা, l2 = 169
বা, l2=(13)2
বা, l = 13
∴ শঙ্কুর তির্যক উচ্চতা 13 সেমি. ।
(xi)দুটি গোলকের বক্রতলের ক্ষেত্রফলের অনুপাত 1:4 হলে , তাদের আয়তনের অনুপাত নির্ণয় কর ।
সমাধানঃ দুটি গোলকের বক্রতলের ক্ষেত্রফলের অনুপাত 1:4 ।
ধরি , গোলকটির ব্যাসার্ধ r 1 একক এবং r2 একক ।
∴ 4π r12 : 4π r22 = 1:4
5.
(i) তোমার কাকার কারখানার একটি মেশিনের মূল্য প্রতি বছর 10 % হারে হ্রাস প্রাপ্ত হয় । মেশিনটির মূল্য 6000 টাকা হলে 3 বছর পরে ওই মেশিনের মূল্য কত হবে ?
সমাধানঃ মেশিনের বর্তমান মূল্য (P ) = 6000 টাকা ।
মেশিনের মূল্য হ্রাসের হার (r) = 10%
সময় (n) = 3 বছর
ধরাযাক , মেশিনটির 3 বছর পর মূল্য হবে A টাকা
∴ মেশিনটির মূল্য 3 বছর পর হবে 4374 টাকা ।
(ii) তিন বন্ধু যথাক্রমে 1,20,000 টাকা , 1,50,000 টাকা ও 1,10,000 টাকা মূলধন নিয়ে একটি বাস ক্রয় করেন । প্রথমজন ড্রাইভার ও বাকি দুজন কন্ডাক্টরের কাজ করেন । তারা ঠিক করেন যে মোট আয়ের 2/5 অংশ তারা কাজের জন্য 3:2:2 অনুপাতে ভাগ করবেন এবং বাকি টাকা মূলধনের অনুপাতে ভাগ করে নেবেন । কোনো একমাসে যদি 29260 টাকা আয় হয় , তবে কে কত টাকা পাবে হিসাব করে লিখি ।
সমাধানঃ তিন বন্ধুর মূলধনের পরিমানের অনুপাত
= 1,20,000:1,50,000:1,10,000
= 12:15:11
তাদের মাসিক আয় = 29260 টাকা
এই লাভের 2/5 অংশ তারা নিজেদের মধ্যে 3:2:2 অনুপাতে ভাগ করে এবং বাকি অংশ মূলধনের অনুপাতে ভাগ করেন ।
লাভের 2/5 অংশ = 2/5 ✕ 29260 টাকা = 11704 টাকা
এখন এই টাকা থেকে
লাভের বাকি অংশ = (29260 – 11704) টাকা = 17556 টাকা
এই টাকা তারা মূলধনের অনুপাতে ভাগ করবেন
∴ ড্রাইভার মোট পাবে = (5016+5544) টাকা = 10560 টাকা
প্রথম কন্ডাক্টর মোট পাবে = (3344+6930) টাকা = 10274 টাকা
দ্বিতীয় কন্ডাক্টর মোট পাবে = (3344+5082 ) টাকা = 8426 টাকা
Madhyamik 2020 Math Question Solution
6.
সমাধানঃ
বা, (x-3)(x+5) = 48
বা, x2-3x+5x-15-48 = 0
বা, x2 +2x -63 =0
বা, x2 –( 9-7)x-63=0
বা, x2 -9x +7x -63=0
বা, x(x-9) +7(x-9) =0
বা, (x-9)(x+7) =0
দুটি রাশির গুনফল শূন্য
∴ (x-9)=0
বা, x =9
এবং (x+7) =0
বা, x = -7
∴ নির্ণেয় সমাধান 9 এবং -7
(ii) দুটি ক্রমিক ধনাত্মক অযুগ্ম সংখ্যার গুনফল 143 হলে সমীকরণটি গঠন করে এবং শ্রীধর আচার্যের সূত্র প্রয়োগ করে সংখ্যা দুটি নির্ণয় কর ।
সমাধানঃ ধরি, দুটি ক্রমিক অযুগ্ম সংখ্যা হল x এবং x+2
শর্তানুসারে ,
X(x+2) = 143
বা, x2 +2x -143 = 0
সমীকরণটিকে ax2 +bx+c =0 সমীকরণের সাথে তুলনা করে পাই ,
a = 1 ,b = 2 এবং c = -143
∴ b2-4ac = (2)2 -4(1)(-143) =4+ 572 = 576 >0
∴ সমীকরণটির বীজদ্বয় বাস্তব ।
শ্রীধর আচার্যের সূত্র প্রয়োগ করে পাই ,
∴ x = 11 এবং x =13
∴ সংখ্যা দুটি হল 11 এবং 11+2 =13
7.
সমাধানঃ x=2+√3
এবং (x+y) =4
∴ y = 4-x
বা, y = 4-(2+√3)
বা, y = (2-√3)
∴ xy = (2+√3)(2-√3) =(2)2 –(√3)2 = 4-3 =1
= 1+1
= 2
(ii) a∝ b এবং b∝c হলে ,প্রমাণ কর যে , a3+b3+c3 ∝ 3abc
সমাধানঃ
A ∝ b
∴ a = pb [যেখানে p একটি অশূন্য ভেদ ধ্রুবক ]
আবার , b ∝ c
∴ b = qc [যেখানে q একটি অশূন্য ভেদ ধ্রুবক ]
∴ a = pb =p(qc) =pqc = rc [ যেখানে pq = r = অশূন্য ভেদ ধ্রুবক ]
= ধ্রুবক
∴ a3+b3+c3 ∝ 3abc [প্রমাণিত ]
8
(i) X:a =y:b =z:c হলে দেখাও যে
সমাধানঃ
ধরি , X:a =y:b =z:c =k [ k(≠0) একটি সমানুপাতিক ধ্রুবক ]
∴ x= ak , y = bk এবং z = ck
বামপক্ষঃ
ডানপক্ষঃ
= 3k3
∴ বামপক্ষ = ডানপক্ষ [ প্রমাণিত ]
Madhyamik 2020 Math Question Solution
Madhyamik 2020 Math Question Solution|মাধ্যমিক ২০২০ গণিত সমাধান|মাধ্যমিক ২০২০ গণিত প্রশ্ন উত্তর
9.
(i) প্রমাণ কর যে একই বৃত্তাংশস্থ সকল কোণের মাণ সমান ।
পাঠ্য বইয়ের (গণিত প্রকাশ দশম শ্রেণী) উপপাদ্য 35 দেখ ।
(ii) প্রমাণ কর , বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে যে দুটি স্পর্শক অঙ্কন করা যায় তাদের স্পর্শবিন্দু দুটির সঙ্গে বহিঃস্থ বিন্দুর সংযোজক সরলরেখাংশ দৈর্ঘ্য দুটির সমান ।
পাঠ্য বইয়ের (গণিত প্রকাশ দশম শ্রেণী) উপপাদ্য 41 দেখ ।
Madhyamik 2020 Math Question Solution|মাধ্যমিক ২০২০ গণিত সমাধান|মাধ্যমিক ২০২০ গণিত প্রশ্ন উত্তর
10.
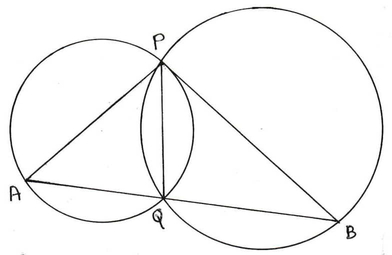
(i)দুটি বৃত্ত পরস্পরকে P ও Q বিন্দুতে ছেদ করেছে । PA ও PB যথাক্রমে দুটি বৃত্তের ব্যাস হলে , প্রমান কর A ,Q ও B বিন্দুত্রয় সমরেখ ।
দুটি বৃত্ত পরস্পরকে P ও Q বিন্দুতে ছেদ করেছে , PA ও PB যথাক্রমে দুটি বৃত্তের ব্যাস প্রমান করেতে হবে যে A , Q ও B বিন্দুত্রয় সমরেখ ।
অঙ্কনঃ P ,Q যুক্ত করা হল ।
প্রমানঃ APQ ত্রিভুজে , AP ব্যাস ।
∴ ∠AQP = 90° [ যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ ]
আবার , ∆BQP ত্রিভুজে , PB ব্যাস
∴ ∠PQB = 90° [ যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ ]
এখন , ∠AQB
=∠AQP+∠PQB
=90°+90°
=180°
∴ A ,Q ও B একই সরলরেখায় অবস্থিত ।
∴ A ,Q ও B সমরেখ ।
Madhyamik 2020 Math Question Solution|মাধ্যমিক ২০২০ গণিত সমাধান|মাধ্যমিক ২০২০ গণিত প্রশ্ন উত্তর
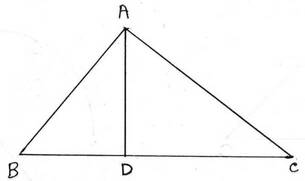
প্রমাণঃ ABC সমকোণী ত্রিভুজের ∠BAC সমকোণ এবং সমকৌণিক বিন্দু A থেকে BC এর উপর AD লম্ব । যেহেতু সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অঙ্কন করলে লম্বের উভয়পার্শ্বে যে দুটি ত্রিভুজ উৎপন্ন হয় তারা পরস্পর সদৃশ এবং প্রত্যেকটি ত্রিভুজ মূল ত্রিভুজের সাথে সদৃশ ।
∴ ∆ABC এবং ∆DAC পরস্পর সদৃশ
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
11.
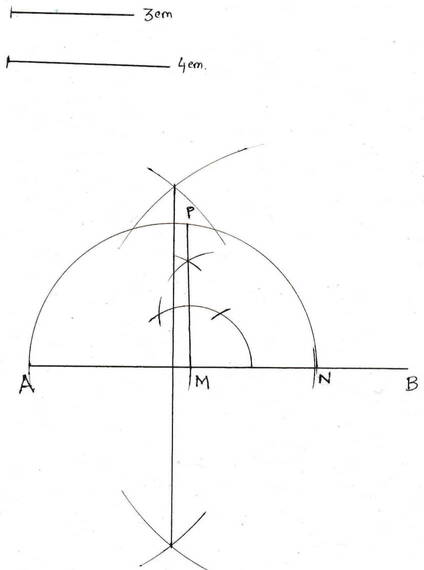
(i) 4 সেমি. ও 3 সেমি. দৈর্ঘ্যের সরলরেখাংশ দুটির মধ্য সমানুপাতী অঙ্কন কর ।
সমাধানঃ
∴ নির্ণেয় মধ্যসমানুপাতীটি হল PM যার দৈর্ঘ্য 3.5সেমি. ।
Madhyamik 2020 Math Question Solution|মাধ্যমিক ২০২০ গণিত সমাধান|মাধ্যমিক ২০২০ গণিত প্রশ্ন উত্তর
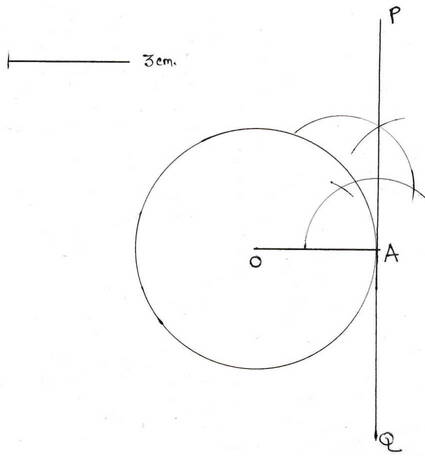
(ii) 3 সেমি ব্যাসার্ধের একটি বৃত্ত অঙ্কন কর । বৃত্তের উপর A বিন্দুতে স্পর্শক অঙ্কন কর ।
∴ A বিন্দুতে অঙ্কিত স্পর্শকটি হল PQ
Madhyamik 2020 Math Question Solution|মাধ্যমিক ২০২০ গণিত সমাধান|মাধ্যমিক ২০২০ গণিত প্রশ্ন উত্তর
12.
সমাধানঃ
(ii) দুটি কোণের সমষ্টি 135° এবং তাদের অন্তর π/12 হলে , কোণ দুটির ষষ্টিক ও বৃত্তীয় মান লিখি ।
সমাধানঃ ধরি , কোণ দুটি হল A এবং B
∴ A+B = 135° —–(i)
এবং A-B = π/12
বা, A-B = 15° —(ii)
(i) ও (ii) নং সমীকরণ যোগ করে পাই ,
A+B +A-B = 135°+15°
বা, 2A = 150°
বা, A = 150°/2
বা, A = 75°
A এর প্রাপ্ত মান (i) নং সমীকরনে বসিয়ে পাই ,
75°+B = 135°
বা, B = 135°-75°
বা, B = 60°
∴ Aও B কোণের ষষ্টিক মান যথাক্রমে 75° এবং 60°
Madhyamik 2020 Math Question Solution
(iii) মান নির্ণয় করঃ
13.
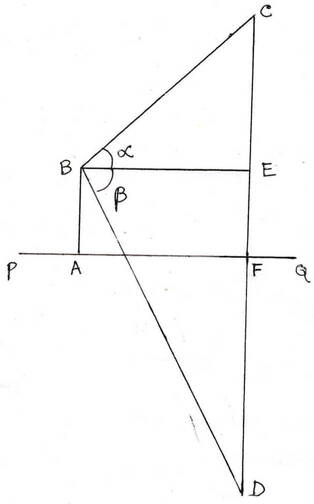
সমাধানঃ
ধরাযাক , PQ হ্রদের A বিন্দু থেকে h উচ্চতায় B বিন্দু থেকে c বিন্দুতে অবস্থিত মেঘের উন্নতি কোণ α আবার B বিন্দু থেকে মেঘের প্রতিবিম্বের অবনতি কোণ β ।
∴ ∠CBE =α এবং ∠EBD = β
B বিন্দু থেকে PQ এর সমান্তরাল সরলরেখা টানা হল যা CD বাহুকে E বিন্দুতে ছেদ করে ।
BEC সমকোণী ত্রিভুজ থেকে পাই ,
∴ BE tanα =CE —(i)
আবার সমকোণী ত্রিভুজ BED থেকে পাই ,
বা, DE = BE tanβ
বা, DF+FE = BE tanβ
বা, CF+AB = BE tan β [ যেহেতু হ্রদ থেকে মেঘের দূরত্ব এবং হ্রদ থেকে প্রতিবিম্বের দূরত্ব সমান ∴ CF=FD এবং AB = EF =h মিটার । ]
বা, CE+EF+AB = BE tanβ
বা, CE +h+h =BE tanβ
বা, CE+2h = BEtanβ
বা, BEtanα +2h = BEtanβ
বা, 2h = BEtanβ-BEtana
বা, 2h = BE(tanβ-tanα)
Madhyamik 2020 Math Question Solution
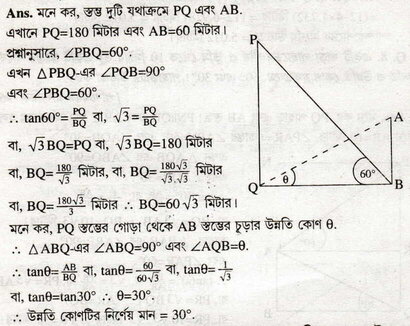
(ii) দুটি স্তম্ভের উচ্চতা যথাক্রমে 180 মিটারও 60 মিটার।দ্বিতীয় স্তম্ভটির গোড়া থেকে প্রথম চূড়ার উন্নতি কোণ 60°হলে ,প্রথমটির গোড়া থেকে দ্বিতীয় চূড়ার উন্নতি কোণ নির্ণয় কর ।
Madhyamik 2020 Math Question Solution|মাধ্যমিক ২০২০ গণিত সমাধান|মাধ্যমিক ২০২০ গণিত প্রশ্ন উত্তর
14. (i) একটি লম্ব বৃত্তাকার চোঙাকৃতি নলের বহির্ব্যাসার্ধের দৈর্ঘ্য 5 সেমি. এবং অন্তর্ব্যাসার্ধের দৈর্ঘ্য 4 সেমি. । নলটির সমগ্রতলের ক্ষেত্রফল 1188 বর্গসেমি হলে ,নলটির দৈর্ঘ্য নির্ণয় করো ।
সমাধানঃ ধরি , নলটির দৈর্ঘ্য h সেমি. ।
নলটির বহির্ব্যাসার্ধ (R ) = 5 সেমি.
নলটির অন্তর্ব্যাসার্ধ (r) = 4 সেমি.
নলটির সমগ্রতলের ক্ষেত্রফল
= {2πRh+2πrh+π(R2-r2)h } বর্গসেমি.
শর্তানুসারে ,
বা, 396h+396 =8316
বা, 396h = 8316-396
বা, 396h = 7920
∴ নলটির দৈর্ঘ্য 20 সেমি. ।
Madhyamik 2020 Math Question Solution|মাধ্যমিক ২০২০ গণিত সমাধান|মাধ্যমিক ২০২০ গণিত প্রশ্ন উত্তর
(ii) 9 সেমি. অন্তর্ব্যাসার্ধ বিশিষ্ট একটি অর্ধ গোলাকার পাত্র সম্পূর্ণ জলপূর্ণ আছে । এই জল 3 সেমি. ব্যাস এবং 4 সেমি. উচ্চতা বিশিষ্ট চোঙাকৃতি বোতলে ভর্তি করে রাখা হবে । পাত্রটি খালি করতে কতগুলি এইরূপ বোতল দরকার তা নির্ণয় কর ।
সমাধানঃ অর্ধ গোলকের ব্যাসার্ধ (R ) = 9 সেমি.
∴ অর্ধ গোলাকৃতি পাত্রের আয়তন
চোঙাকৃতি বোতলের ব্যাস 3 সেমি. ।
∴ বোতলের ব্যাসার্ধ (r ) = 3/2 সেমি.
বোতলের উচ্চতা (h) = 4 সেমি.
∴ চোঙাকৃতি বোতলের আয়তন
= πr2h ঘন সেমি.
ধরি , পাত্রটি খালি করতে x টি বোতলের প্রয়োজন হবে ।
∴পাত্রের পাত্রের জলের আয়তন = x টি বোতলের জলের আয়তন
বা, 486 = 9x
বা, x = 486/9
বা, x = 54
∴ পাত্রটি খালি করতে 54 টি বোতলের প্রয়োজন হবে ।
Madhyamik 2020 Math Question Solution|মাধ্যমিক ২০২০ গণিত সমাধান|মাধ্যমিক ২০২০ গণিত প্রশ্ন উত্তর
(iii)একটি লম্ব বৃত্তাকার শঙ্কুর ভূমিতলের ব্যাস 21 মিটার এবং উচ্চতা 14 মিটার । প্রতিও বর্গ মিটার 1.50 টাকা হিসাবে পার্শ্বতল রঙ করতে কত খরচ পড়বে ?
সমাধানঃ লম্ব বৃত্তাকার শঙ্কুর ব্যাস 21 মিটার
∴ লম্ব বৃত্তাকার শঙ্কুর ব্যাসার্ধ (r ) = 21/2 সেমি.
লম্ব বৃত্তাকার শঙ্কুর উচ্চতা (h) = 14 মিটার ।
ধরি , লম্ব বৃত্তাকার শঙ্কুর তির্যক উচ্চতা l সেমি.
∴ l2 = h2+r2
∴ শঙ্কুর পার্শ্বতলের ক্ষেত্রফল
15.
(i) ছাত্রীদের প্রাপ্ত নম্বরের গড় নির্ণয় কর যদি তাদের প্রাপ্ত নম্বরের ক্রমযৌগিক পরিসংখ্যা নিম্নরূপ হয়
| নম্বর | ছাত্রী সংখ্যা |
| 10 এর কম | 6 |
| 20 এর কম | 10 |
| 30 এর কম | 18 |
| 40 এর কম | 30 |
| 50 এর কম | 46 |
সমাধানঃ এখানে দেখা যাচ্ছে যে 6 জন 10 এর কম পেয়েছে , অর্থাৎ 0-10 এর মধ্যে পেয়েছে 6 জন । আবার 10 জন 20 এর কম পেয়েছে, সুতরাং 10-20 এর মধ্যে পেয়েছে (10-6) জন = 4 জন । এভাবে পরিসংখ্যা তালিকাটি তৈরি করলে তা হবে
| নম্বর | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| ছাত্রী সংখ্যা | 6 | 4 | 89 | 12 | 16 |
এক্ষেত্রে a = 25 এবং h = 10 ধরে পাই ,
| শ্রেণী সীমানা | পরিসংখ্যা (fi) | শ্রেণী মধ্যক (xi) | ui = (xi-a)/10 | fiui |
| 0-10 | 6 | 5 | -2 | -12 |
| 10-20 | 4 | 15 | -1 | -4 |
| 20-30 | 8 | 25 = a | 0 | 0 |
| 30-40 | 12 | 35 | 1 | 12 |
| 40-50 | 16 | 45 | 2 | 32 |
| মোট | ∑fi = 46 | ∑fiui =28 |
ছাত্রীদের প্রাপ্ত নম্বরের গড়
(ii) নীচের পরিসংখ্যা বিভাজন থেকে তথ্যটির মধ্যমা নির্ণয় করি ।
| শ্রেণী সীমানা | পরিসংখ্যা |
| 0-10 | 4 |
| 10-20 | 7 |
| 20-30 | 10 |
| 30-40 | 15 |
| 40-50 | 10 |
| 50-60 | 8 |
| 60-70 | 5 |
সমাধানঃ
পরিসংখ্যা বিভাজন তালিকাটি হল
| শ্রেণি সীমানা | পরিসংখ্যা | ক্রমযৌগিক পরিসংখ্যা (ক্ষুদ্রতর সূচক ) |
| 0-10 | 4 | 4 |
| 10-20 | 7 | 11 |
| 20-30 | 10 | 21 |
| 30-40 | 15 | 36 |
| 40-50 | 10 | 46 |
| 50-60 | 8 | 54 |
| 60-70 | 5 | 59 = n |
এখানে n = 59
∴ n/2 = 59/2 =29.5
29.5 এর থেকে ঠিক বেশি ক্রমযৌগিক পরিসংখ্যা (30-40) শ্রেণীর মধ্যে আছে ।
সুতরাং মধ্যমা শ্রেণীটি হল (30-40)
∴ নির্ণেয় মধ্যামা
(iii) নীচের শ্রেণী –বিন্যাসিত পরিসংখ্যা বিভাজনের সংখ্যাগুরু মান নির্ণয় কর ।
| শ্রেণী | পরিসংখ্যা |
| 1-6 | 2 |
| 6-9 | 6 |
| 9-12 | 12 |
| 12-15 | 24 |
| 15-18 | 21 |
| 18-21 | 12 |
| 21-24 | 3 |
সমাধানঃ
উপরের পরিসংখ্যা বিভাজনের সংখাগুরুমান শ্রেণীটি হল 12-15 ।
∴ নির্ণেয় সংখ্যাগুরুমান
= 12 +4
= 16 [উত্তর ]
ধন্যবাদ । যদি আপনাদের এই POST টি ভালো লাগে তাহলে SHARE করার অনুরোধ রইল । এই রকম আরও সুন্দর সুন্দর POST পাওয়ার জন্য আমাদের website টি LIKE করুন।
source-Anushilan.com
©kamaleshforeducation.in(2023)