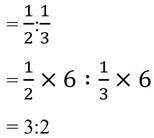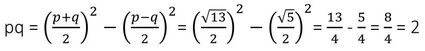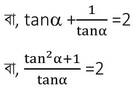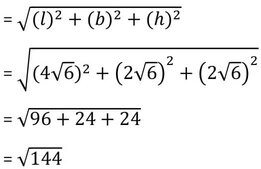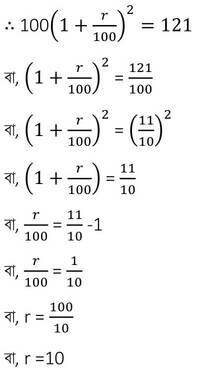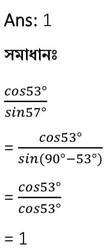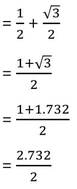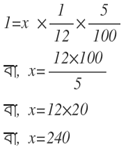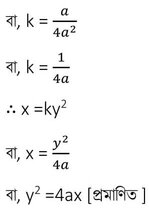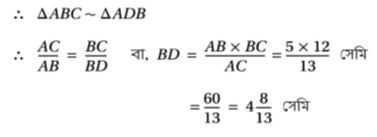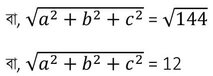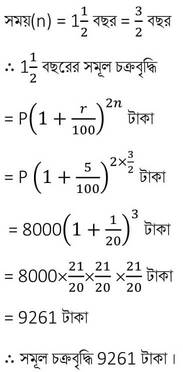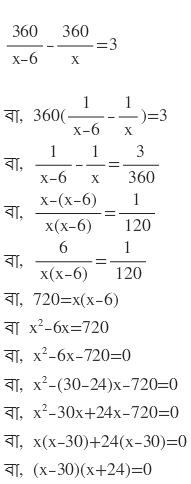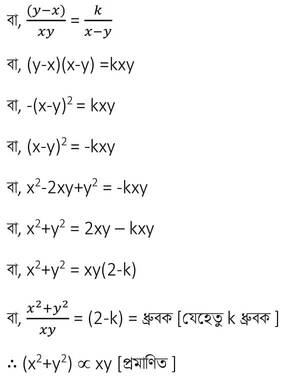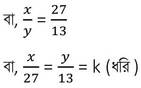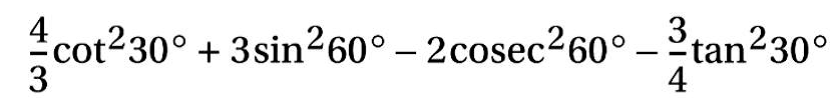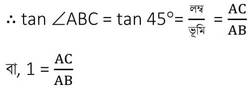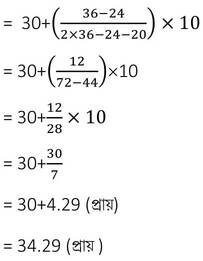Madhyamik 2019 Math Question Solution

মাধ্যমিক ২০১৯ গণিত প্রশ্নের সমাধান।
1.নিম্নলিখিত প্রশ্ন গুলির প্রতিটি ক্ষেত্রে সঠিক উত্তর নির্বাচন করঃ
(i) কোনো অংশীদারি ব্যাবসায় দুই বন্ধুর প্রাপ্ত লভ্যাংশের অনুপাত 1/2 : 1/3 হলে , তাঁদের মূলধনের অনুপাত-
(a) 2:3
(b) 3:2
(c) 1:1
(d) 5:3
Ans: (b) 3:2
সমাধানঃ আমরা জানি কোনো অংশীদারি ব্যাবসায় মূলধনের অনুপাত এবং লভ্যাংশের অনুপাত সমান হয় ।
∴ এক্ষেত্রে মূলধনের অনুপাত হবে
(ii) যদি p+q = √13 এবং p-q = √5 হয় , তাহলে pq এর মান —
(a) 2
(b) 18
(c) 9
(d) 8
Ans: (a) 2
সমাধানঃ
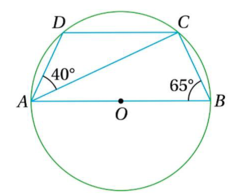
(iii) কোনো বৃত্তের কেন্দ্র O এবং ব্যাস AB । ABCD বৃত্তস্থ চতুর্ভুজ । ∠ABC =65° , ∠DAC=40°হলে ∠BCD এর মান—
(a) 75°
(b) 105°
(c ) 115°
(d) 80°
Ans: (c ) 115°
সমাধানঃ
∠ACB অর্ধ বৃত্তস্থ কোণ
∴ ∠ACB = 90°
∴ ∠BAC = 180°-(∠ACB+∠ABC)=180°-(90°+65°)=180°-155°= 25°
∴ ∠DAB = ∠DAC+∠BAC = 40°+25°=65°
আমরা জানি বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক
∴ ∠DAB+∠BCD =180°
বা, 65° +∠BCD = 180°
বা, ∠BCD = 180°-65°
বা, ∠BCD = 115°
(iv) tana+cota =2 হলে, (tan13a +cot13a ) –এর মান
(a) 13
(b) 2
(c ) 1
(d) 0
Ans: (c ) 2
সমাধানঃ tana+cota =2
বা, tan2α +1 = 2tanα
বা, tan2α -2tanα +1 =0
বা, (tanα-1)2 =0
বা, (tanα-1) =0
বা, tanα =1
∴ (tan13α +cot13α)
= (1)13 +(1)13
= 1+1
= 2 [উত্তর]
(v) 2√6 সেমি বাহু বিশিষ্ট দুটি ঘনক পাশাপাশি রাখলে উৎপন্ন আয়তঘনকটির কর্ণের দৈর্ঘ্য হবে —–
(a) 10 সেমি.
(b) 6 সেমি.
(c) 2 সেমি.
(d) 12 সেমি.
Ans: (d) 12 সেমি.
সমাধানঃ 2√6 সেমি বাহু বিশিষ্ট দুটি ঘনক পাশাপাশি রাখলে উৎপন্ন আয়তঘনকটির দৈর্ঘ্য (l) = 2√6+2√6 = 4√6 সেমি .
প্রস্থ (b) =2√6 সেমি.
উচ্চতা (h) = 2√6 সেমি.
∴ আয়তঘনকটির কর্ণের দৈর্ঘ্য হবে
=12 cm.
(vi) x1,x2,x3,…….,x10 রাশিগুলির গড় 20 হলে x1+4 ,x2+4 ,………, x10+4 রাশিগুলির গড় হবে –
(a) 20
(b) 24
(c) 40
(d) 10
Ans: (b) 24
সমাধানঃ x1,x2,x3,…….,x10 রাশিগুলির গড় 20
2. শূন্যস্থান পূরণ করঃ
(i) এক ব্যাক্তি ব্যাঙ্কে 100 টাকা জমা রেখে , 2 বছর পর সমূল চক্রবৃদ্ধি পেলেন 121 টাকা । বার্ষিক সুদে হার ছিল _________ % ।
Ans:
সমাধানঃ ধরি , বার্ষিক সুদের হার r %
∴ বার্ষিক সুদের হার 10%
(ii) দুটি দ্বিঘাত করণীর যোগফল ও গুনফল একটি মুলদ সংখ্যা হলে করনীদ্বয় ______ করণী ।
Ans: অনুবন্ধী করণী
(iii) দুটি ত্রিভুজের ভূমি একই সরলরেখায় অবস্থিত এবং ত্রিভুজ দুটির অপর শীর্ষবিন্দু সাধারণ হলে , ত্রিভুজ দুটির ক্ষেত্রফলের অনুপাত ভূমির দৈর্ঘ্যের অনুপাতের ___________ ।
Ans: সমান
(v) একটি নিরেট লম্ব বৃত্তাকার চোঙের তলসংখ্যা _______ ।
Ansঃ 3 টি
(vi) x1,x2,………,x100 চলগুলি উর্দ্ধক্রমে থাকলে এদের মধ্যমা __________ ।
সমাধানঃ
Madhyamik 2019 Math Question Solution|Madhyamik 2019 Math Question Paper|মাধ্যমিক ২০১৯ গণিত প্রশ্নের সমাধান
3. সত্য বা মিথ্যা লেখ ।
(i) বার্ষিক 10% হারে 100 টাকার 1 বছরের সরল সুদ ও চক্রবৃদ্ধি সুদের পার্থক্য 1 টাকা ।
উত্তরঃ মিথ্যা ।
সমাধানঃ এক্ষেত্রে আসল (P) = 100টাকা
সুদের হার (r ) = 10 %
সময় (t) = 1 বছর
সরল সুদ ও চক্রবৃদ্ধি সুদ সমান ।
(ii) ab:c2 , bc:a2 , ca:b2 –এর যৌগিক অনুপাত 1:1 ।
উত্তরঃ সত্য ।
সমাধানঃ
ab:c2 , bc:a2 , ca:b2 –এর যৌগিক অনুপাত
= (ab)(bc)(ca) = c2a2b2
= a2b2c2 : c2b2c2
= 1:1
(iii) তিনটি অসমরেখ বিব্দু দিয়ে একটি মাত্র বৃত্ত অঙ্কন করা যায় ।
উত্তরঃ সত্য
(iv) sin30° +sin60° > sin90°
উত্তরঃ সত্য।
সমাধানঃ
sin30° +sin60°
= 1.366 > 1 =sin90°
(v) একই ভূমি ও একই উচ্চতা বিশিষ্ট একটি লম্ব বৃত্তাকার শঙ্কু ও একটি লম্ব বৃত্তাকার চোঙের আয়তনের অনুপাত হবে 1:3
উত্তরঃ 1:3
সমাধানঃ ধরি , লম্ব বৃত্তাকার শঙ্কু ও লম্ব বৃত্তাকার চোঙের ব্যাসার্ধ r একক এবং উচ্চতা h একক ।
∴ এদের আয়তনের অনুপাত
= 1:3
(vi) 2,3,9,10,9,3,9 তথ্যের মধ্যমার মান 10 ।
Ans: মিথ্যা ।
সমাধানঃ সংখ্যা গুলিকে মানের উর্দ্ধক্রমে সাজিয়ে পাই ,
2 ,3,3,9,9,9,10
এক্ষেত্রে n = 7
∴ মধ্যমা = (n+1)/2 তম মান = 8/2 তম মান = 4 তম মান = 9
4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাও ।
(i) বার্ষিক 5 % সরল সুদের হারে কত টাকার মাসিক সুদ এক টাকা তা নির্ণয় করি ।
সমাধান
ধরি আসল= x টাকা
শর্তানুসারে ,
∴ মাসিক সুদ 240 টাকা ।
(ii) একটি অংশীদারী ব্যাবসায় তিনজনের মূলধনের অনুপাত 3:5:8 । প্রথম ব্যাক্তির লাভ তৃতীয় ব্যাক্তির লাভের থেকে 60 টাকা কম হলে ব্যাবসায় মোট কত টাকা লাভ হয়ে ছিল ।
সমাধানঃ ধরি , বাবসায় মোট লাভ হয়েছিল x টাকা ।
বা, x = 192
∴ ব্যাবসায় মোট লাভ 192 টাকা ।
∴ P =11
(iv) x ∝ y2 এবং y =2a , x =a হলে দেখাও যে y2=4ax ।
সমাধানঃ
x ∝ y2
বা, x =ky2
বা, a = k(2a)2
বা, a = k (4a2)
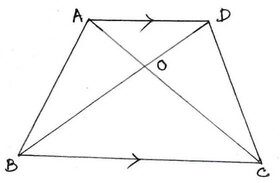
∆AOD ও ∆COB এর ক্ষেত্রে ,
∠OAD = ∠OCD [ একান্তর কোণ,যেহেতু, AD||BC এবং AC ভেদক ]
আবার,∠ODA=∠OCB [একান্তর কোণ,যেহেতু,AD||BC এবং DB ভেদক ]
∠AOD=∠BOC [বিপ্রতীপ কোন]
∴ ∆AOD এবং ∆COB সদৃশকোণী।যেহেতু, সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতী,
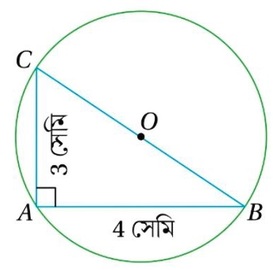
(vi) একটি বৃত্তে দুটি জ্যা AB ও AC পরস্পর লম্ব । AB= 4 সেমি. এবং AC =3সেমি. হলে, বৃত্তটির ব্যাসার্ধের দৈর্ঘ্য নির্ণয় কর ।
সমাধানঃ
যেহেতু , AB এবং AC জ্যা দুটি পরস্পর লম্ব সুতরাং ACB সমকোণী ত্রিভুজ । AB = 4 সেমি. ও AC = 3 সেমি.
যেহেতু ∠BAC =90
∴ BC হল ব্যাস
∴ ব্যাসার্ধ = BC/2 = 5/2 সেমি. =2.5 সেমি.
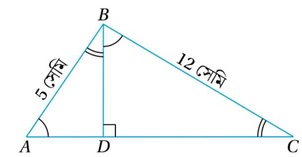
(vii) ABC একটি সমকোণী ত্রিভুজের ∠ABC =90° এবং BD⊥AC , যদি AB= 5 সেমি. এবং BC=12 সেমি. হয় তবে BD এর দৈর্ঘ্য নির্ণয় কর ।
সমাধানঃ
ABC সমকোণী ত্রিভুজে,
আবার ABC ত্রিভুজের ∠ABC = 90 এবং সমকৌণিক বিন্দু B থেকে অতিভুজ AC এর উপর BD লম্ব । । যেহেতু সমকোণী ত্রিভুজের সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অঙ্কন করলে যে দুটি ত্রিভুজ উৎপন্ন হয় তারা মূল ত্রিভুজের সঙ্গে সদৃশ ।
∴ BD = (4 পূর্ণ 8/13) সেমি.
(viii) ϴ(0° ≤ ϴ ≤ 90° ) –এর কোন মান বা মানগুলির জন্য 2sinϴ cosϴ = cosϴ হবে ?
সমাধানঃ 2sinϴ cosϴ = cosϴ
বা, 2sinϴ cosϴ -cosϴ =1
বা, cosϴ (2sinϴ-1) =0
∴ cosϴ = 0
বা, cosϴ = cos90°
বা, ϴ =90°
অথবা ,
(2sinϴ-1)=0
বা, sinϴ = ½
বা, sinϴ = sin30°
বা, ϴ= 30°
∴ ϴ এর মান গুলি হল 90° এবং 30° ।
(ix) sin10ϴ =cos8ϴ এবং 10ϴ ধনাত্মক সূক্ষ্মকোণ হলে , tan 9ϴ এর মান নির্ণয় কর ।
সমাধানঃ
sin10ϴ =cos8ϴ
বা, sin 10ϴ= sin(90°-8ϴ)
বা, 10ϴ = 90° – 8ϴ
বা, 10ϴ+8ϴ = 90°
বা, 18ϴ = 90°
বা, ϴ = 90°/18
বা, ϴ =5°
∴ tan 9ϴ
= tan(9✕5°)
= tan 45°
= 1
(x)একটি আয়তঘনাকৃতি ঘরের দৈর্ঘ্য ,প্রস্থ ও উচ্চতা যথাক্রমে a, b এবং c একক এবং a+b+c= 25, ab+bc+ca = 240.5 হলে ঘরটির মধ্যে যে বৃহত্তম দণ্ডটি রাখা যাবে তাঁর দৈর্ঘ্য নির্ণয় কর ।
সমাধানঃ
a+b+c =25 এবং ab+bc+ca=240.5
এখন , a2+b2+c2 =(a+b+c)2-2(ab+bc+ca)
বা, a2+b2+c2 = (25)2 -2(240.5) =625-481 = 144
∴ আয়তঘনাকৃতি ঘরের কর্ণের দৈর্ঘ্য 12 একক অর্থাৎ ওই ঘরে সর্বাপেক্ষা যে লম্বা দণ্ডটি রাখা যাবে তার মান 12 একক ।
(xi ) একটি লম্ব বৃত্তাকার শঙ্কুর পার্শ্বতলের ক্ষেত্রফল ভূমির ক্ষেত্রফলের √5 গুন । শঙ্কুটির উচ্চতা ও ভূমির ব্যাসার্ধের অনুপাত নির্ণয় কর ।
সমাধানঃ ধরি, লম্ব বৃত্তাকার শঙ্কুর ব্যাসার্ধ r একক , উচ্চতা h একক এবং তির্যক উচ্চতা l একক ।
∴ লম্ব বৃত্তাকার শঙ্কুর পার্শ্বতলের ক্ষেত্রফল = πrl বর্গ একক এবং ভূমিতলের ক্ষেত্রফল πr2 বর্গ একক
শর্তানুসারে,
πrl = √5✕πr2
বা, l = r√5
বা, l2 = 5r2 [ উভয়পক্ষে বর্গ করে পাই ]
বা, h2+r2 = 5r2 [ l2=h2+r2 ]
বা, h2 = 4r2
বা, h2/r2 = 4:1
বা, h/r = 2/1 [ উভয়পক্ষে বর্গমূল করে পাই ]
বা, h:r = 2:1
∴ শঙ্কুটির উচ্চতা ও ব্যাসার্ধের অনুপাত 2:1 ।
(xii) প্রথম (2n+1) সংখ্যক ক্রমিক স্বাভাবিক সংখ্যার মধ্যবর্তী সংখ্যা (n+103)/3 হলে , n এর মা নির্ণয় কর ।
সমাধানঃ প্রথম (2n+1) সংখ্যক ক্রমিক স্বাভাবিক সংখ্যার মধ্যবর্তী সংখ্যা =(n+1) তম সংখ্যা =(n+1)
∴ (n+1) =(n+103)/3
বা, 3n+3 = n+103
বা, 3n-n = 103-3
বা, 2n = 100
বা, n = 100/2
বা, n = 50
∴ n =50
5.
সমাধানঃ আসল (P) = 8000 টাকা
সুদের হার (r) = 10%
6 মাস অন্তর সুদ আসলের সঙ্গে যুক্ত হয় সুতরাং চক্রবৃদ্ধি সুদের পর্ব = 2
এবং চক্রবৃদ্ধি সুদ = সমূল চক্রবৃদ্ধি – আসল = (9261 – 8000)টাকা = 1261 টাকা ।
(ii) 14. দুই বন্ধু যথাক্রমে 40000 টাকা ও 50000 টাকা দিয়ে একটি যৌথ ব্যাবসা শুরু করেন ।তাদের মধ্যে একটি চুক্তি হয় যে লাভের 50% নিজেদের মধ্যে সমান ভাগে এবং লাভের অবশিষ্ট অংশ মূলধনের অনুপাতে ভাগ হবে । প্রথম বন্ধুর লভ্যাংশের পরিমান যদি দ্বিতীয় বন্ধুর লভ্যাংশ অপেক্ষা 800 টাকা কম হয় , তবে প্রথম বন্ধুর লভ্যাংশ কত ?
সমাধানঃ দুই বন্ধুর মুলধনের অনুপাত = 40000:50000 =4:5
ধরি , মোট লাভ = x টাকা ।
এখন , তাদের মধ্যে চুক্তি অনুযায়ী লাভের 50 % তাদের মধ্যে সমান ভাগে ভাগ হয় এবং বাকি অংশ মূলধনের অনুপাতে ভাগ হয় ।
6.
(i) x2+x+1 =0 সমীকরণের বীজগুলির বর্গ যে সমীকরনের বীজ ,সেই সমীকরণটি নির্ণয় কর ।
সমাধানঃ ধরি, x2+x+1 =0 সমীকরনের বীজগুলি হল a এবং b. আমাদের যে সমীকরণটি নির্ণয় করতে হবে তার বীজগুলি প্রদত্ত সমীকরণের বীজগুলির বর্গ হবে অর্থাৎ a2 এবং b2 বীজ বিশিষ্ট দ্বিঘাতসমীকরণ নির্ণয় করতে হবে ।
x2+x+1 =0 সমীকরনের বীজগুলি হল a এবং b
∴ a+b = -1 এবং ab = 1
এখন , a2+b2
= (a+b)2-2ab
= (-1)2-2(1) [যেহেতু ,a+b = -1 এবং ab = 1]
= 1-2
=-1
এবং a2b2 = (ab)2 =(1)2 =1[∵ab = 1]
নির্ণেয় সমীকরণটি হল ,
x2-(a2+b2)x+a2b2=0
= x2-(-1)x+1=0
= x2+x+1
∴ x2+x+1 এই সমীকরণটি হল সেই সমীকরণ যার বীজগুলি প্রদত্ত দ্বিঘাত সমীকরণের বীজগুলির বর্গ ।
Madhyamik 2019 Math Question Solution
মাধ্যমিক ২০১৯ গণিত প্রশ্নের সমাধান।
(ii) 9. কলমের মূল্য প্রতি ডজনে 6 টাকা কমলে 30 টাকায় আরো তিনটি বেশি কলম পাওয়া যাবে । কমার পূর্বে প্রতি ডজন কলমের মূল্য নির্ণয় করি ।
সমাধানঃ
ধরি প্রতি ডজন কলমের মূল্য x টাকা ।
∴ x টাকায় পাওয়া যাবে 12 টি কলম
1 টাকায় পাওয়া যাবে 12/x টি কলম
30 টাকায় পাওয়া যাবে (30×12)/x টি কলম =360/x টি কলম ।
এখন প্রতি ডজন কলমের মূল্য (x-6) টাকা
∴ (x-6) টাকায় পাওয়া যায় 12 টি কলম
1 টাকায় পাওয়া যায় 12/(x-6) টি কলম
30 টাকায় পাওয়া যায় (30× 12)/(x-6) টি কলম =360/(x-6) টি কলম ।
শর্তানুসারে ,
দুটি রাশির গুনফল শূন্য
∴ হয় (x-30)=0
বা, x=30
অথবা, (x+24)=0
বা, x=-24
কলমের মূল্য ঋণাত্মক হতে পারেনা , সুতরাং x=30
অর্থাৎ প্রতি ডজন কলমের মূল্য 30 টাকা ।
7.
(i)
8.
(i) (3x-2y) : (x+3y) = 5:6 হলে, (2x+5y) : (3x+4y) নির্ণয় কর ।
সমাধানঃ
(3x-2y) : (x+3y) = 5:6
বা, 6(3x-2y) = 5(x+3y)
বা, 18x-12y = 5x+15y
বা, 18x-5x = 12y+15y
বা, 13x = 27y
[k (≠0) একটি সমানুপাতিক ধ্রুবক ]
∴ x = 27k এবং y = 13k
∴ (2x+5y) : (3x+4y)
= {2(27k)+5(13k)} : {3(27k) +4(13k)}
= (54k+65k) : ( 81k+52k)
= 119k : 133k
= 119:133
= 17 : 19
∴ (2x+5y) : (3x+4y)= 17 : 19
9.
(i) অর্ধ – বৃত্তস্থ কোন সমকোণ – প্রমাণ কর ।
গণিত প্রকাশ বইয়ের (দশম শ্রেণী) উপপাদ্য-37 দেখ ।
(ii) প্রমাণ কর যে , যদি দুটি বৃত্ত পরস্পরকে বহিঃস্পর্শ করে , তাহলে স্পর্শ বিন্দুটি কেন্দ্র দুটির সংযোজক সরল্রেখাংশের ওপর অবস্থিত হবে ।
গণিত প্রকাশ বইয়ের (দশম শ্রেণী) উপপাদ্য-42 দেখ ।
Madhyamik 2019 Math Question Solution
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
মাধ্যমিকের সকল বিষয়ের বিগত বছরের প্রশ্ন উত্তর (Click Here)
10.
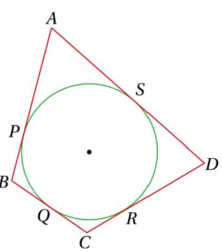
(i) O কেন্দ্রীয় বৃত্তের পরিলিখিত চতুর্ভুজ ABCD হলে প্রমাণ কর যে , AB+CD = BC +DA
ধরাযাক ABCD চতুর্ভুজটির AB ,BC,CD এবং DA বাহুগুলি বৃত্তটিকে যথাক্রমে P ,Q,R এবং S বিন্দুতে স্পর্শ করেছে । প্রমাণ করতে হবে যে , AB+CD = BC +DA
A বিন্দু থেকে দুটি স্পর্শক AP ও AS টানা হয়েছে ।
∴ AP =AS –(i)
B বিন্দু থেকে দুটি স্পর্শক BP ও BQ অঙ্কন করা হয়েছে
∴ BP = BQ –(ii)
আবার , C বিন্দু থেকে দুটি স্পর্শক CQ ও CR অঙ্কন করা হয়েছে ।
∴ CQ = CR –(iii)
এবং D বিন্দু থেকে দুটি স্পর্শক DS ও DR অঙ্কন অরা হয়েছে
∴ DS =DR —(iv)
এখন AB+CD
= AP+PB +CR+RD
= AS+BQ+CQ+DS [(i) ,(ii) ,(iii) ও (iv) থেকে পাই ]
= (AS+DS) + (BQ+CQ)
= AD+BC [প্রমাণিত ]
Madhyamik 2019 Math Question Solution
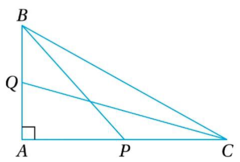
(ii) ABC –এর A সমকোণ এবং BP ও CQ দুটি মধ্যমা হলে , প্রমাণ কর যে , 5BC2 = 4(BP2+CQ2)
ত্রিভুজ ABC-এর ∠A সমকোণ এবং BP ও CQ দুটি মধ্যমা , প্রমাণ করতে হবে যে 5BC2 = 4(BP2+CQ2)
প্রমাণঃ ABC একটি সমকোণী ত্রিভুজ যার ∠A সমকোণ
∴ BC2
= AB2+AC2
= (2AQ)2 +(2AP)2 [ যেহেতু P ও Q যথাক্রমে AC ও AB এর মধ্যবিন্দু ]
= 4AQ2 +4AP2
আবার সমকোণী ত্রিভুজ BAP ও CAQ থেকে পাওয়া যায় ,
BP2 = AP2+AB2
বা, BP2 = AP2 + (2AQ)2
বা, BP2 = AP2 +4AQ2
এবং CQ2 = AC2 +AQ2
বা, CQ2 = (2AP)2+AQ2
বা, CQ2 = 4AP2 +AQ2
∴ BP2 +CQ2
= AP2 +4AQ2 +4AP2 +AQ2
= 5AP2 +5AQ2
= 5(AP2+AQ2)—(ii)
∴ 5BC2
= 5(4AQ2 +4AP2 ) [(i) থেকে পাই ]
= 4.{5(AQ2+AP2)}
= 4 (BP2 +CQ2) [(ii) থেকে পাই ] [ প্রমাণিত ]
Madhyamik 2019 Math Question Solution|Madhyamik 2019 Math Question Paper Solved|Madhyamik 2019 Math Question Answer|মাধ্যমিক ২০১৯ গণিত প্রশ্নের সমাধান।
11.
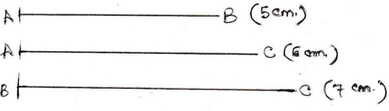
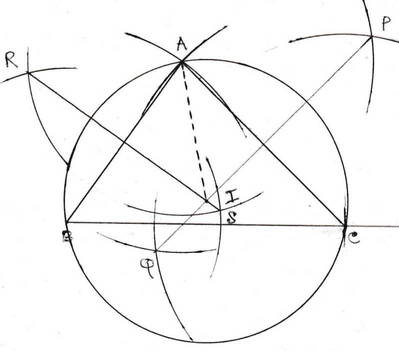
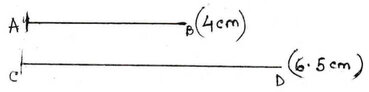
(i) ABC একটি ত্রিভুজ অঙ্কন করো যার BC = 7 সেমি. , AB = 5সেমি. এবং AC =6সেমি. । ABC ত্রিভুজটির পরিবৃত্ত অঙ্কন করো । (কেবলমাত্র অংকন চিহ্ন দিতে হবে )
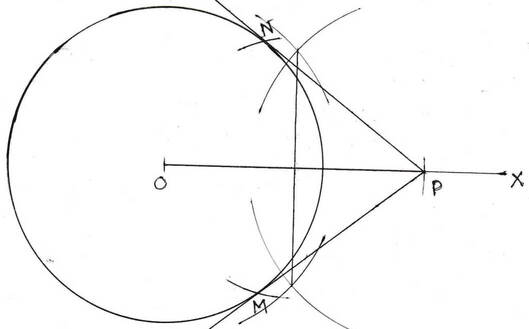
(ii) 4 সেমি ব্যাসার্ধ বিশিষ্ট একটি বৃত্ত অংকন করো । বৃত্তের কেন্দ্র থেকে 6.5 সেমি দূরে কোনো বহিঃস্থ বিন্দু থেকে ওই বৃত্তের দুটি স্পর্শক অংকন করো ।
বহিঃস্থ বিন্দু থেকে দুটি স্পর্শক PN এবং PM অংকন করা হল ।
12.
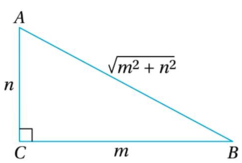
সমাধানঃ
ABC ত্রিভুজের C =90º এবং BC=m একক এবং AC = n একক
(ii)
সমাধানঃ
Madhyamik 2019 Math Question Solution
13.
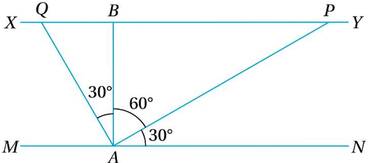
(i) 600 মিটার চওড়া কোনো নদীর একটি ঘাট থেকে দুটি নৌকা ভিন্ন অভিমুখে নদীর ওপারে যাওয়ার জন্য রওনা দিল । যদি প্রথম নৌকাটি নদীর এপারের সঙ্গে 30° কোণ এবং দ্বিতীয় নৌকাটি প্রথম নৌকার গতিপথের সঙ্গে 90° কোণ করে চলে ওপারে পৌঁছায় তাহলে ওপারে পৌঁছানোর পরে নৌকা দুটির দূরত্ব কত হবে ?
সমাধানঃ
ধরা যাক , MN পাড়ের A বিন্দুস্থ ঘাট থেকে প্রথম নৌকা AP পথে গিয়ে নদীর অপর পাড় XY –এর P বিন্দুতে এবং দ্বিতীয় নৌকা AQ পথে গিয়ে Q বিন্দুতে ওপারে পৌঁছায় ।
AB = নদীর চওড়া = 600 মিটার ।
সুতরাং , ∠PAN = 30°, ∠PAQ = 90°
∴ ∠PAB = 60° এবং ∠BAQ =30°
PQ = নৌকা দুটির দূরত্ব
বা, BP = √3 AB =√3´600
বা, BP = 600√3
∴ PQ = BP+QB = (600√3 + 200√3)মিটার = 800√3 মিটার
∴ নৌকা দুটির দূরত্ব 800√3 মিটার ।
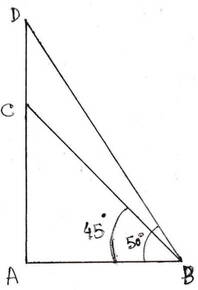
(ii) একটি তিনতলা বাড়ির ছাদে 3.6 মিটার দৈর্ঘ্যের একটি পতাকা আছে । রাস্তার কোনো এক স্থান থেকে দেখলে পতাকা দণ্ডটির চূড়া ও পাদদেশের উন্নতি কোণ যথাক্রমে 50° ও 45° হয় । তিনতলা বাড়ির উচ্চতা হিসাব করে লিখি । [ধরে নাও tan50° = 1.2 ]
সমাধানঃ
AC হল তিনতলা বাড়ির উচ্চতা এবং CD হল পতাকার দৈর্ঘ্য ।রাস্তার উপর একটি বিন্দু B থেকে পতাকার পাদদেশের অর্থাৎ C বিন্দুর উন্নতি কোণ 45 এবং B বিন্দু থেকে পতাকার চূড়া অর্থাৎ D বিন্দুর উন্নতি কোণ 50।
∴CD =3.6 এবং ∠ABC = 45° এবং ∠ABD = 50°
এখন , ABC ত্রিভুজে ∠BAC =90° এবং ∠ABC =45°
বা, AB =AC —(i)
আবার , ABD ত্রিভুজে ∠BAD = 90° এবং ∠ABD = 50°
বা, 1.2AC = AC+3.6
বা, 1.2AC-AC=3.6
বা, 0.2AC = 3.6
বা, AC =
বা, AC = 18
∴ তিনতলা বাড়ির উচ্চতা 18 মিটার ।
Madhyamik 2019 Math Question Solution
14.
(i) ঘনকাকৃতি একটি সম্পূর্ণ জলপূর্ণ চৌবাচ্চা থেকে সমান মাপের 64 বালতি জল তুলে নিলে চৌবাচ্চাটির 1/3 অংশ জলপূর্ণ থাকে । চৌবাচ্চাটির একটি ধারের দৈর্ঘ্য 1.2 মিটার হলে প্রতিটি বালতিতে কত লিটার জল ধরে হিসাব করে লিখি । ( 1 ঘনডেসিমিটার = 1 লিটার )
সমাধানঃ ঘনকাকৃতি জলপূর্ণ চৌবাচ্চাটির আয়তন
= 1.2✕1.2✕1.2 ঘন মিটার
= 1.728 ঘন মিটার
= 1728 ঘন ডেসিমি
= 1728 লিটার
সমগ্র চৌবাচ্চাটির 1/3 অংশ
= 1/3 ✕ 1.728 ঘনমিটার
= 0.576 ঘন মিটার
= 576 ঘন ডেসিমি
= 576 লিটার
চৌবাচ্চাটি থেকে তুলে নেওয়া জলের পরিমান
= 1728-576
= 1152 লিটার
ধরি প্রতিটি বালতিতে জলধরে = x লিটার
∴64বালতিতে জল ধরে 64x লিটার
শর্তানুসারে ,
64x = 1152
বা, x = 1152 /64
Or, x= 18
∴ প্রতিটি বালতিতে 18 লিটার জল ধরে ।
Madhyamik 2019 Math Question Solution
(ii) একটি তারের প্রস্থচ্ছেদের ব্যাস 50% কমানো হল । আয়তন অপরিবর্তিত রাখতে হলে তারটির দৈর্ঘ্য কত শতাংশ বাড়াতে হবে ?
সমাধানঃ ধরি , তারের প্রস্থচ্ছেদের ব্যাসার্ধ r একক এবং দৈর্ঘ্য h একক ।
∴ ব্যাস = 2r একক
তারের প্রস্থচ্ছেদের ব্যাস 50% কমানো হলে , পরিবর্তিত ব্যাস হবে
= (2r-r) একক
= r একক
∴ পরিবর্তিত ব্যাসার্ধ = r/2 একক
পূর্বে তারটির আয়তন ছিল = πr2h ঘন একক
ধরা যাক , আয়তন অপরিবর্তিত রাখতে হলে তারটির দৈর্ঘ্য হবে H একক
∴ তারটির দৈর্ঘ্য 300% বৃদ্ধি করতে হবে ।
Madhyamik 2019 Math Question Solution|Madhyamik 2019 Math Question Paper Solved|Madhyamik 2019 Math Question Answer|মাধ্যমিক ২০১৯ গণিত প্রশ্নের সমাধান।
(iii) 6. লম্ব বৃত্তাকার শঙ্কু আকৃতির একটি তাঁবু তৈরি করতে 77 বর্গ মিটার ত্রিপল লেগেছে । তাঁবুটির তির্যক উচ্চতা যদি 7 মিটার হয় ,তবে তাঁবুটির ভূমির ক্ষেত্রফল হিসাব করে লিখি ।
সমাধানঃ লম্ব বৃত্তাকার শঙ্কু আকৃতির একটি তাঁবু তৈরি করতে 77 বর্গ মিটার ত্রিপল লেগেছে ।
অর্থাৎ তাঁবুটির পার্শ্ব তলের ক্ষেত্রফল 77 বর্গ মিটার।
তাঁবুটির তির্যক উচ্চতা (l) = 7 মিটার ।
ধরি, তাঁবুটির ভূমিতলের ব্যাসার্ধ r মিটার ।
শর্তানুসারে ,
πrl = 77
উত্তরঃ তাঁবুটির ভূমিতলের ক্ষেত্রফল 38.5 বর্গ সেমি.।
Madhyamik 2019 Math Question Solution
15.
(i) যদি নীচের পরিসংখ্যা বিভাজন তালিকার যৌগিক গড় 54 হয় , তবে K এর মান নির্ণয় করঃ
| শ্রেণী | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 |
| পরিসংখ্যা | 7 | 11 | K | 9 | 13 |
সমাধানঃ
| শ্রেণী | পরিসংখ্যা (fi) | শ্রেণী মধ্যক (xi) | fixi |
| 0-20 | 7 | 10 | 70 |
| 20-40 | 11 | 30 | 330 |
| 40-60 | K | 50 | 50k |
| 60-80 | 9 | 70 | 630 |
| 80-100 | 13 | 90 | 1170 |
| ∑fi = 40+k | ∑ fixi = 2220+50k |
∴ k =10
(ii) নীচের প্রদত্ত ক্রমযৌগিক পরিসংখ্যা বিভাজন ছকটি থেকে পরিসংখ্যা বিভাজন ছক তৈরি করে তথ্যতির সংখ্যাগুরু মান নির্ণয় করঃ
| শ্রেণী | 10-এর কম | 20-এর কম | 30-এর কম | 40-এর কম | 50-এর কম | 60-এর কম | 70-এর কম | 80-এর কম |
| পরিসংখ্যা | 4 | 16 | 40 | 76 | 96 | 112 | 120 | 125 |
সমাধানঃ প্রদত্ত ক্রমযৌগিক পরিসংখ্যা থেকে পরিসংখ্যা বিভাজন ছক তৈরি করা হলঃ
| শ্রেণি সীমানা | পরিসংখ্যা |
| 0-10 | 4 |
| 10-20 | 16-4=12 |
| 20-30 | 40-16=24 |
| 30-40 | 76-40=36 |
| 40-50 | 96-76=20 |
| 50-60 | 112-96=16 |
| 60-70 | 120-112=8 |
| 70-80 | 125-120=5 |
সংখ্যাগুরু মান সম্বলিত শ্রেণীটি হল (30-40) ।
যেখানে , l = সংখ্যাগুরু শ্রেণীর নিম্নসীমানা = 30
f1 = সংখ্যাগুরু শ্রেণীর পরিসংখ্যা = 36
f0 = সংখ্যাগুরু শ্রেণীর ঠিক পূর্ববর্তী শ্রেণীর পরিসংখ্যা = 24
f2 = সংখ্যাগুরু স্রেনির ঠিক পরবর্তী স্রেনির পরিসংখ্যা = 20
h = শ্রেণী দৈর্ঘ্য = 10
∴ সংখ্যাগুরুমান
(iii) নীচের তালিকা থেকে একটি বিদ্যালয়ের দশম শ্রেণীর 52 জন ছাত্রের গড় নম্বর প্রত্যক্ষ পদ্ধতি ও কল্পিত গড় পদ্ধতিতে নির্ণয় করঃ
| ছাত্র সংখ্যা | 4 | 7 | 10 | 15 | 8 | 5 | 3 |
| নম্বর | 30 | 33 | 35 | 40 | 43 | 45 | 48 |
সমাধানঃ
| বছর (xi) | ছাত্র সংখ্যা (fi) | fixi | Di = xi-a = xi-40 | fidi |
| 30 | 4 | 120 | -10 | -40 |
| 33 | 7 | 231 | -7 | -49 |
| 35 | 10 | 350 | -5 | -50 |
| 40=a | 15 | 600 | 0 | 0 |
| 43 | 8 | 344 | 3 | 24 |
| 45 | 5 | 225 | 5 | 25 |
| 48 | 3 | 144 | 8 | 24 |
| মোট | ∑fi = 52 | ∑ fixi = 2014 | ∑ fidi =-66 |
প্রত্যক্ষ পদ্ধিতিতে , গড় নম্বর = 2014/52 = 78.73 (প্রায় )
কল্পিত গড় (a) = 40 (ধরা হল )
ধন্যবাদ । POST টি ভালো লাগলে SHARE করার অনুরোধ রইল।
source-AN
©kamaleshforeducation.in(2023)