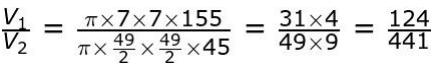Skip to content




CBSE Class 10 Maths Additional Practice Questions 2024 PDF…
CBSE Class 10 Maths Practice Questions & Solutions
Here we have provided the CBSE Class 10 Maths
Additional Practice Question Paper with answers
Section A – MCQs
Q1. Which of the following could be the graph of the polynomial?
(x – 1)²(x + 2)?…
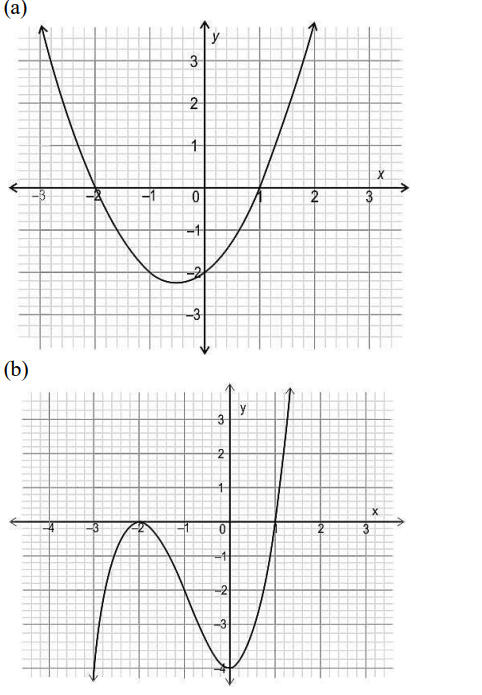
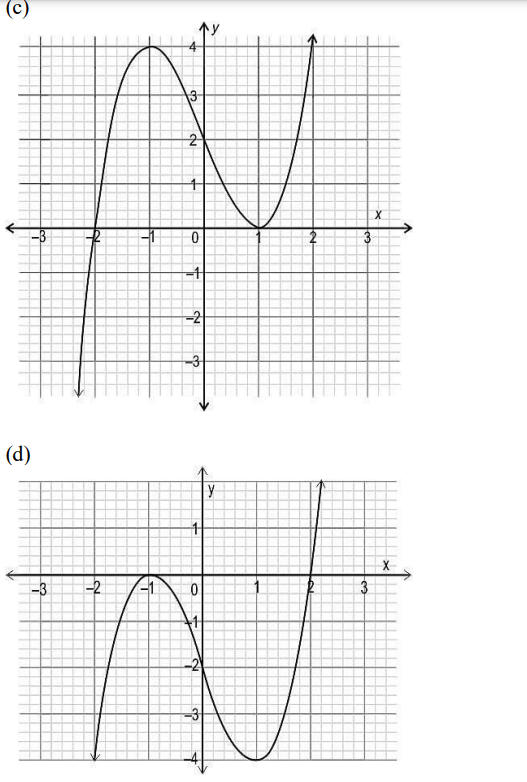
Answer- (c)…
Q 2: The lines k1, k2, and k3 represent three different equations as shown in the graph below. The solution of the equations represented by the lines k1 and k3 is x = 3 and y = 0 while the solution of the equations represented by the lines k2 and k3 is x = 4 and y = 1…. Read more at: https://www.careerpower.in/school/question-paper/cbse-class-10-mathematics-additional-practice-questions-2023-24
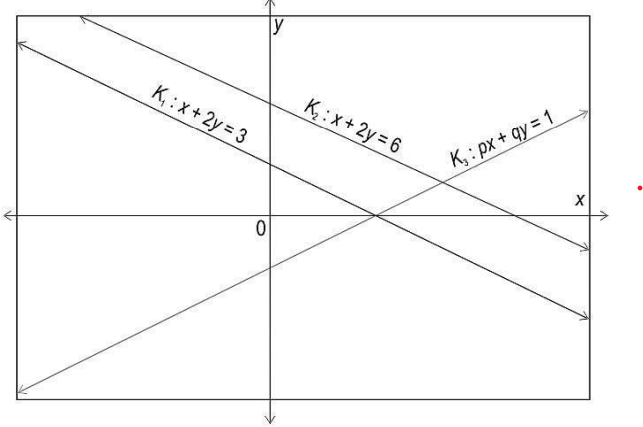
Which of these is the equation of the line k3?
(a) x – y = 3
(b) x – y = -3
(c) x + y = 3
(d) x + y = 1
Answer- (a) x – y = 3
Q3: What is/are the roots of 3x² = 6x?
(a) only 2
(b) only 3
(c) 0 and 6
(d) 0 and 2
Answer- (d) 0 and 2
Q4: The coordinates of the center of the circle, O, and a point on the circle, N, are shown in the figure below.
.
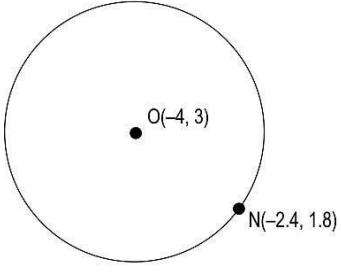
What is the radius of the circle?
(a) √0.4 units
(b) 2 units
(c) 4 units
(d) √42.4
Answer- (b) 2 units
Q5: ΔPQR is shown below. ST is drawn such that ∠PRQ = ∠STQ….
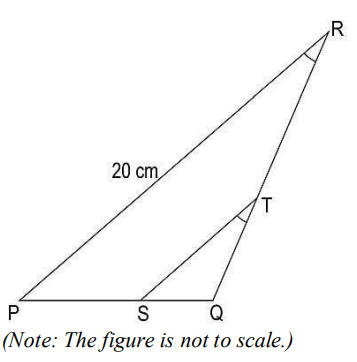
If ST divides QR in a ratio of 2:3, then what is the length of ST?
(a) 10/3cm
(b) 8 cm
(c) 12 cm
(d) 40/3cm
Answer- (b) 8 cm
Q6: Two scalene triangles are given below….
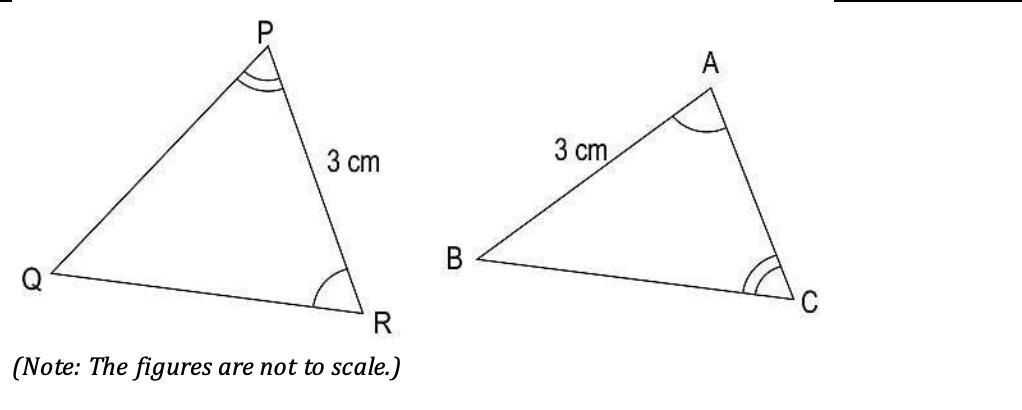
Anas and Rishi observed them and said the following: Anas: ΔPQR is similar to ΔCBA Rishi: ΔPQR is congruent to ΔCBA Which of them is/are correct?
(a) Only Anas
(b) Only Rishi
(c) Both Anas and Rishi
(d) Neither of them, as two scalene triangles can never be similar or congruent.
Answer- (a) Only Anas
Q7: Harsha made a wind chime using a frame and metal rods. She punched 8 holes in the frame, each 2 cm apart, and then hung 6 metal rods from the frame, as shown in the figure below. The ends of the metal rods are aligned over a line, shown by the dotted line in the figure….
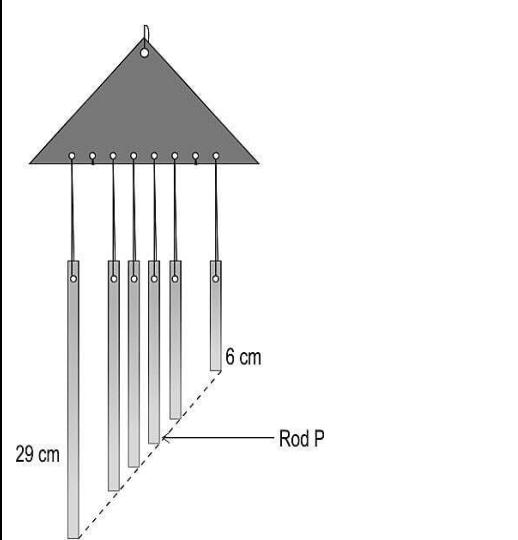
If all of the rods are straight and not swaying, then what is the length of Rod P?
(a) 69/7 cm
(b) 53/5 cm
(c) 76/5 cm
(d) 111/7 cm
Answer- (d) 111/7 cm
Q8. Two circles with centers O and N touch each other at point P as shown. O, P, and N are collinear. The radius of the circle with center O is twice that of the circle with center N. OX is tangent to the circle with center N, and OX = 18 cm….
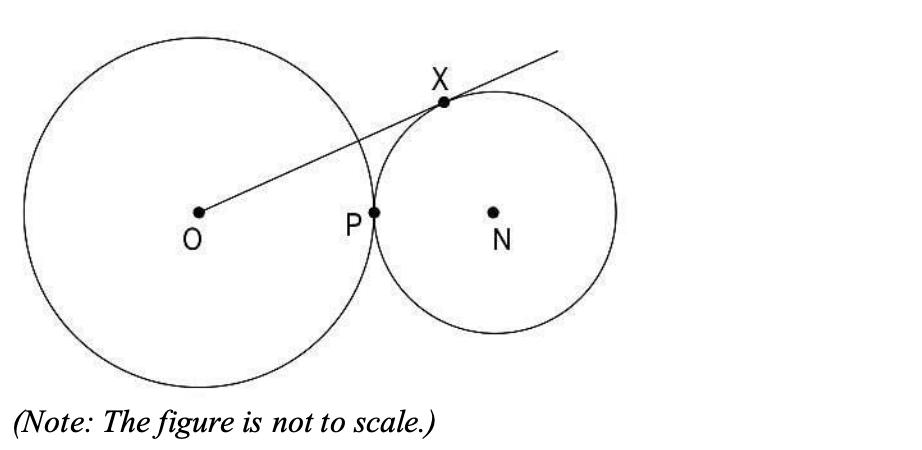
What is the radius of the circle with center N?
(a) 18/√2 cm
(b) 9 cm
(c) 9/√2 cm
(d) 18/√10 cm
Answer- (c) 9/√2 cm
Q9. Shown below is a circle with center O having tangents at points P, T, and S….
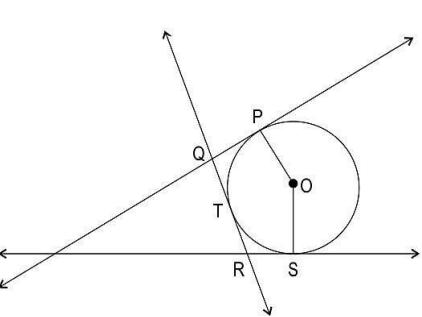
(Note: The figure is not to scale.)
If QR = 12 cm and the radius of the circle is 7 cm, what is the perimeter of the polygon PQTRSO?
(a) 26 cm
(b) 31 cm
(c) 38 cm
(d) (cannot say with the given information.)
Answer. (c) 38 cm
Q10. Shown below is a table with values of cosecant and secant of different angles….
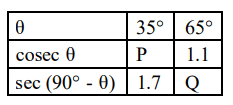
What are the values of P and Q respectively?
(a) 1/1.7 and 1/1.1
(b) 1.1 and 1.7
(c) 1.7 and 1.1
(d) (cannot be found with the given information)
Answer. (c) 1.7 and 1.1
Q11. In the figure below, PQRS is a square….
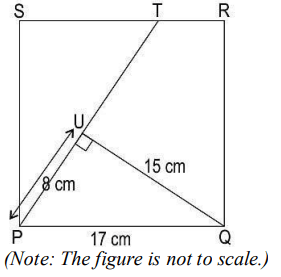
What is the value of sin ∠SPT?
(a) 8/17
(b) 8/15
(c)15/17
(d) (cannot be found with the given information)
Answer. (a) 8/17
Q12. Shown below is a solved trigonometric problem….

In which step is there an error in solving?
(a) Step 1
(b) Step 2
(c) Step 3
(d) There is no error.
Answer. (a) step 1
Q13. A circle with radius 6 cm is shown below. The area of the shaded region in the circle is of the area of the circle.
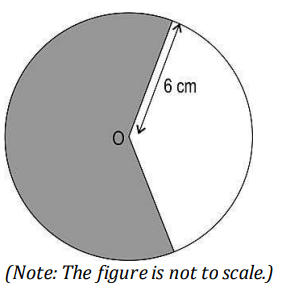
What is the length of the circle’s minor arc?
(a) 16𝜋/3cm
(b) 20𝜋/3cm
(c) 16π cm
(d) 20π cm
Answer. (a) 16𝜋/3cm
Q14. A regular pentagon is inscribed in a circle with centre O, of radius 5 cm, as shown below…
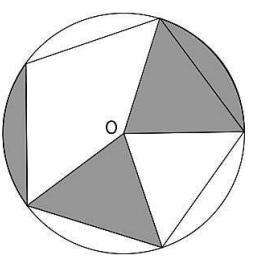
What is the area of the shaded part of the circle?
(a) 2π cm²
(b) 4π cm²
(c) 5π cm²
(d) 10π cm²
Answer. (d) 10π cm²
Q15. A cuboid of base area P sq units is filled with water up to a height of Q units. A sphere of volume R cu units is dropped into the cuboid such that it is completely submerged. A representation of the submerged sphere is shown below….
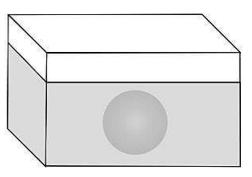
Which of these represents the increase in the height of water?
(a) 0 units
(b) 𝑅/𝑃 units
(c) R units
(d) 𝑄 + 𝑅/𝑃 units
Answer. (b) 𝑅/𝑃 units
Q16. Sweety, Nitesh, and Ashraf visited a hospital for their annual body checkup, which included a blood pressure evaluation. The results of their systolic blood pressure readings are as follows:
Sweety: 121 mmHg
Nitesh: 147 mmHg
Ashraf: 160 mmHg
The table below depicts the systolic blood pressure ranges of all the patients who visited the hospital on the same day….
Blood Pressure (mmHg) Number of patients
115 – 125 10
125 – 135 9
135 – 145 12
145 – 155 19
155 – 165 10…
Who among the three friends have a blood pressure reading that falls in the modal class?
(a) Sweety
(b) Nitesh
(c) Ashraf
(d) Both Sweety and Ashraf
Answer. (b) Nitesh
Q17. The table below depicts the weight of the students of class 6 of Red Bricks Public School. There are 18 students in the class that weigh above the median weight….
Weight in Kg Number of Students
25 – 28 6
28 – 31 8
31 – 34 7
34 – 37 10
37 – 40 ?…
If there are no students with the same weight as the median weight, how many students weigh between the range of 37 – 40 kgs?
(a) 5
(b) 7
(c) 18
(d) 31
Answer. (a) 5…
Q18. Ginny flipped a fair coin three times and tails came up each time. Ginny wants to flip the coin again.
What is the probability of getting heads in the next coin flip?
(a) 0
(b) 0.25
(c) 0.5
(d) 1
Answer. (c) 0.5
Q19. A number q is prime factorized as 32 × 72 × b, where b is a prime number other than 3 and 7.
Based on the above information, two statements are given below – one labeled Assertion (A) and the other labeled Reason (R). Read the statements carefully and choose the option that correctly describes statements (A) and (R).
Assertion (A): q is definitely an odd number.
Reason (R): 32 × 72 is an odd number.
(a) Both (A) and (R) are true and (R) is the correct explanation for (A).
(b) Both (A) and (R) are true but (R) is not the correct explanation for (A).
(c) (A) is true but (R) is false.
(d) (A) is false but (R) is true.
Answer. (d) (A) is false but (R) is true.
Q20. P (-2, 5) and Q (2, -1) are two points on the coordinate plane.
Two statements are given below – one labeled Assertion (A) and the other labeled Reason (R). Read the statements carefully and choose the option that correctly describes statements (A) and (R).
Assertion (A): The midpoint (0, 2) is the only point equidistant from P and Q.
Reason (R): There are many points (x, y) where (x + 2)2 + (y – 5)2 = (x – 2)2 + (y + 1)2 are equidistant from P and Q.
(a) Both (A) and (R) are true and (R) is the correct explanation for (A).
(b) Both (A) and (R) are true and (R) is not the correct explanation for (A).
(c) (A) is true but (R) is false.
(d) (A) is false but (R) is true.
Answer. (d) (A) is false but (R) is true.
Section B – Very Short Answer Type Questions
Q21. Check whether the statement below is true or false.
“The square root of every composite number is rational.”
Justify your answer by proving rationality or irrationality as applicable.
Answer. Takes a number that is not a perfect square but is a composite number.
For example, 6.
Assumes √6 = 𝑎/𝑏, where b ≠ 0, a, and b are co-primes.
Write b√6 = a and squares on both sides to get 6b² = a².
Writes that as a² is divisible by 2 and 3 which are both prime numbers, a is also divisible by both 2 and 3. Hence concludes that a is divisible by 6.
Write a = 6c, where c is an integer and squares on both sides to get a² = 36c².
Replaces a² with 6b² from step 2 to get 6b² = 36c² and solves it to get b² = 6c².
Writes that as b² is divisible by 2 and 3 which are both prime numbers, b is also divisible by both 2 and 3. Hence concludes that b is divisible by 6.
Writes that 2 and 3 divide both a and b which contradicts the assumption that a and b are co-prime and hence √6 is irrational. Concludes that the given statement is false.
Q22. Kimaya and Heena started walking from point P at the same moment in opposite directions on a 800 m long circular path as shown below. Kimaya walked to the clubhouse at an average speed of 100 m/min and Heena walked to the badminton court at an average speed of 80 m/min. The length of the circular track between the clubhouse and the badminton court is 180
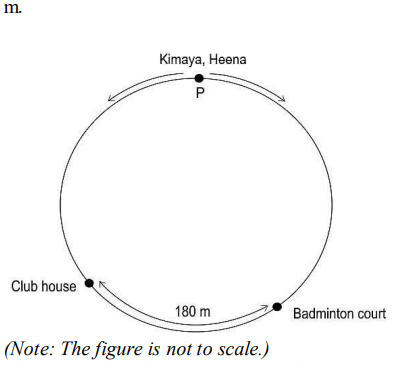
If Heena took 1 minute more than Kimaya to reach her destination, find the time taken by Heena to reach the badminton court. Show your work.
Answer. Assumes the time taken by Kimaya and Heena to reach the club house and the badminton court as t1 and t2 respectively and frames the equation as:
t2 – t1 = 1
Assumes the distance travelled by Kimaya as x m and by Heena as y m and frames the equation for the total distance travelled by Kimaya and Heena together as:
x + y = 800 – 180 = 620
Uses the constant speeds of Kimaya and Heena to find the values of x and y as:
x = 100t1 and y = 80t2
Replaces the values of x and y in the equation of distance travelled as:
100t1 + 80t2 = 620
Substitutes the value of t1 in the above equation as:
100(t2 -1) + 80t2 = 620
Solves the above equation to find the value of t2 as 4 minutes
Q23. Shown below is a circle with centre O and three tangents drawn at points A, E and C. AE is a diameter of the circle. The tangents intersect at points B and D….
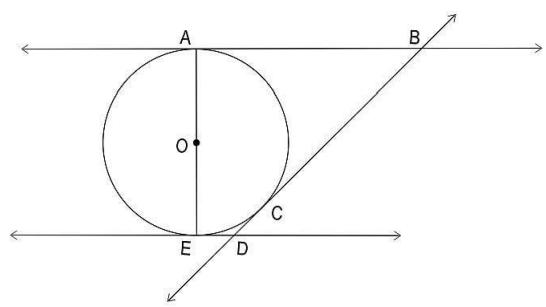
Based on the above information, evaluate whether the following statement is true or false. Justify your answer.
Atleast one pair of opposite sides of AEDB is parallel.
Answer. Writes that the statement is true.
Gives a valid reason. For example, as tangents are drawn at A and E, ∠OAB = ∠OED = 90°. Since these are adjacent interior angles, and are supplementary, AB||ED. Hence, atleast one pair of opposite sides of AEDB is parallel.
Q24. Shown below is a right circular cone of volume 13,600 cm³….
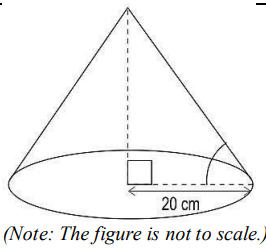
Find the angle which the slant height makes with the base radius. Show your work.
(Note: Take π as 3, √2 as 1.4 and √3 as 1.7.)
Answer. Uses the formula for the volume of a cone and solves for height, h, as:
1/3× 3 × 20 × 20 × h = 13600
=> h = 34 cm
Finds the angle, θ, which the slant height makes with the base radius as:
tan θ = 34/20
=> tan θ = 1.7
=> tan θ = tan 60°
=> θ = 60°
OR
Q24. Shown below are two right triangles….
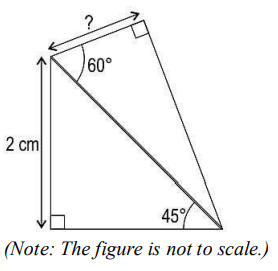
Find the length of the unknown side marked ‘?’. Show your work.
Answer. Writes sin 45° = 2/ℎ𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 and finds the hypotenuse as 2√2 cm.
(Award full marks if it is solved correctly by applying any other properties of triangles.)
Writes cos 60° = 𝑏𝑎𝑠𝑒/2√2 and finds the unknown side marked with ‘?’ as:
2√2 × 1/2 = √2 cm.
Q25. ABCD is a rhombus with side 3 cm. Two arcs are drawn from points A and C respectively such that the radius equals the side of the rhombus. The figure is shown below….
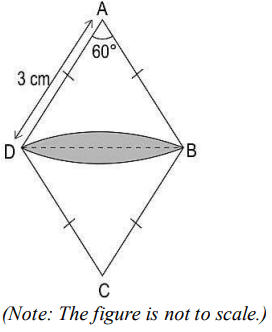
If BD is a line of symmetry for the figure, then find the area of the shaded part of the figure in terms of 𝜋. Show your work.
Answer. Finds the area of sector ABD as 60/360 × π × 3² = 3𝜋/2 cm²
Finds the area of ΔABD as √3/4 × 9 = 9√3/4 cm²
Finds the required area as:
2 × (area of sector ABD – area of ΔABD)
= 2 × (3/2π – 9√3/4)
= 3π – 9√3/2 cm²
OR
Q25. Wasim made a model of Pac-Man, after playing the famous video game of the same name. The area of the model is 120π cm2. Pac-Man’s mouth forms an angle of 60° at the centre of the circle.
A picture of the model is shown below….
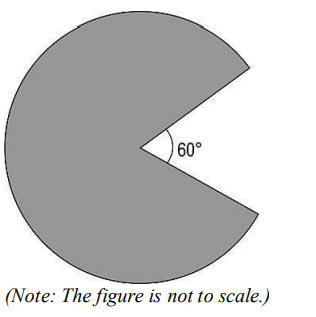
Wasim wants to decorate the model by attaching a colored ribbon to the entire boundary of the shape. What is the minimum length of the ribbon required in terms of? Show your work.
Answer. Assumes the radius of the circle as r cm and writes the equation for the
area as:
120π = 300/360 × π × r²
=> r = 12 cm
Finds the length of ribbon required as:
(300/360 × 2 × π × 12) + 24 cm = (20π + 24) cm.
Section C – Short Answer Type Questions
Q26. Prime factorization of three numbers A, B, and C is given below:
A = (2r × 3p × 5q)
B = (2p × 3r × 5p)
C = (2p × 3q × 5p) such that, p < q < r and p, q, & r are natural numbers..
♦ The largest number that divides A, B, and C without leaving a remainder is
30.
♦ The smallest number that leaves a remainder of 2 when divided by each of
A, B, and C are 5402.
Find A, B, and C. Show your work.
Answer. Finds the HCF and LCM of A, B and C from the prime factorisation as:
HCF = 2p × 3p × 5p
LCM = 2r × 3r × 5q
From the given information, infers that HCF of A, B and C is 30 and equates it to the HCF obtained in step 1 to get the value of p as:
2p × 3p × 5p = 30
=> (2 × 3 × 5)p = (2 × 3 × 5)1
=> p = 1
From the given information, infers that LCM of A, B and C is 5402 – 2 = 5400.
Equates it to the LCM obtained in step 1 to get the values of q and r as:
2r × 3r × 5q = 5400
=> (2 × 3)r × (5)q = (2 × 3)3 × (5)2
=> q = 2 and r = 3
Substitutes the values of p, q, and r to find the values of A, B, and C as:
A = 2³ × 3¹ × 5² = 600
B = 2¹ × 3³× 5¹= 270
C = 2² × 3² × 5¹ = 180
Q27. Riddhi throws a stone in the air such that it follows a parabolic path before it lands at P on the ground as depicted by the graph below….
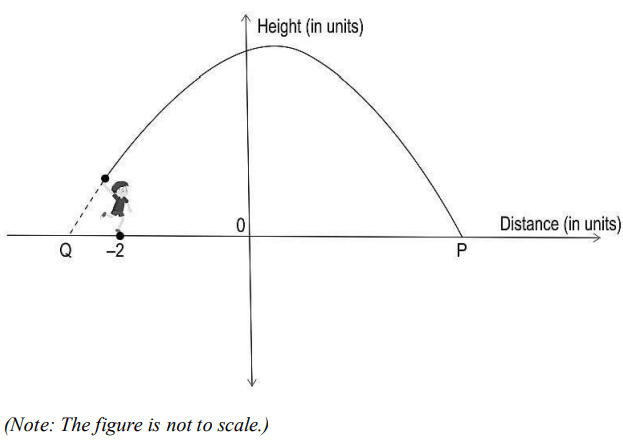
i) The above graph is represented by a polynomial where the sum of its zeroes is 1 and the sum of the squares of its zeroes is 25. Find the coordinates of P and Q.
ii) If one unit on the graph represents 25 metres, how far from Riddhi does the stone land?
Show your work.
Answer. i) Assumes the polynomial to be ax2 + bx + c and considers its zeroes to be α and β.
Given: α + β = 1
α² + β² = 25
Uses the identity (α + β)² to find αβ as (-12).
From the relation between coefficients and zeroes of a polynomial, finds b and c in terms of a as:
b = (-a) and c = (-12a)
Frames the expression of a polynomial as:
ax² – ax – 12a
Assumes the value of a as 1 and factorises the above polynomial as:
x² – x – 12 = (x – 4)(x + 3)
Finds the zeroes as 4 and (-3).
Thus, finds the coordinates of P and Q as (4, 0) and (-3, 0).
ii) Writes that the distance between Riddhi and the point where the stones lands (P) is (2 + 4) = 6 units.
Finds the distance between Riddhi and point P as (6 × 25) = 150 metres.
Q28. Given below is a pair of linear equations:
2x – my = 9
4x – ny = 9
Find at least one pair of the possible values of m and n, if exists, for which the above pair of linear equations has:
i) a unique solution
ii) infinitely many solutions
iii) no solution
Show your work.
Answer. i) Writes that for the equations to have unique solution:
a1 /a2 ≠ b1/b2
Hence in the given equations:
m/n ≠ 2/4 OR m/n ≠ 1/2
Substitutes a set of values for m and n in the given pair of equations which satisfies the above condition and frames a pair of equations. For example:
2x – 2y = 9
4x – 6y = 9
(Award full marks if any other pair of equations satisfying the above conditions is framed.)
ii) Writes that for the equations to have infinitely many solutions:
a1/a2 = b1/b2 = c1/c2
Reasons that in the pair of equations provided:
a1/a2 = 2/4 = 1/2
While c1/c2 = 9/9 = 1
Concludes that as the required condition can never be satisfied, it is not feasible to frame a pair of equations having infinitely many solutions.
iii) Writes that for the equations to have no solution:
a1/a2 = b1/b2 ≠ c1/c2
In the given equations:
c1/c2 which is not equal to a1/a2
Now, substitute a pair of values for m and n in the given equations such that:
m/n = a1/a2 = 1/2
For example,
2x – 3y = 9
4x – 6y = 9
(Award full marks if any other pair of equations satisfying the above conditions is framed.)
OR
Q28. (6, 0) and (0, 2) are two of the points of intersections of two lines represented by a pair of linear equations.
i) How many points of intersections does the pair of linear equations have in total? Justify your answer.
ii) Find the equation that represents one of the lines of the above pair. Show your work.
Answer. i) Writes that the pair will have infinitely many solutions.
Reasons that as there are more than one points of intersection, the pair is of coincident or overlapping lines.
ii) Substitutes the values of the point of intersection (6, 0) in the equation
of a line ax + by = c as:
6a + 0 = c
or a = 𝑐/6
Substitutes the values of the second point of intersection (0, 2) in the equation as:
2b = c
or b = 𝑐/2
Rewrites the equation of a line by substituting the values of a and b in
terms of c as:
𝑐/6x + 𝑐/2y = c
Simplifies the above equation by taking c = 1 to find the equation of the line as x + 3y = 6.
Q29. In the given figure, PQ is the diameter of the circle with centre O. R is a point on the boundary of the circle, at which a tangent is drawn. A line segment is drawn parallel to PR through O, such that it intersects the tangent at S….
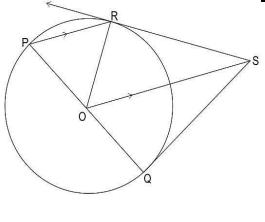
Show that SQ is a tangent to the circle.
Answer. Finds that ∠OPR = ∠ORP, and ∠ORP = ∠ROS.
Finds ∠QOS = ∠ROS = ∠ORP. Gives a valid reason. For example:
Using exterior angle property, ∠OPR + ∠ORP = ∠QOS + ∠ROS.
=> 2∠ROS = ∠QOS + ∠ROS
=> ∠QOS = ∠ROS
Writes that ΔORS ≅ ΔOQS by SAS congruence. The working may look as follows:
OS = OS (common side)
OR = OQ (radius)
∠ROS = ∠QOS
Note that as RS is a tangent to the circle, ∠ORS = 90°.
Concludes that SQ is a tangent to the circle as ∠ORS = ∠OQS = 90°, by CPCT.
OR
Q29. Shown below is a circle with centre O. Tangents are drawn at points A and C, such that they intersect at point B.
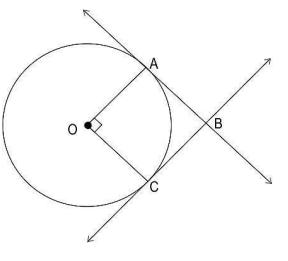
If OA ⊥ OC, then show that quadrilateral OABC is a square.
Answer. Writes that AB = BC, as they are tangents from an external point to a circle.
Notes that OA = OC as they are radii.
Writes that ∠BAO = ∠BCO = 90° as AB and BC are tangents.
Notes that OA || BC as ∠AOC + ∠OCB = 180° (adjacent interior angles)
Notes that OC || AB as ∠AOC + ∠OAB = 180° (adjacent interior angles)
Concludes that OABC is a parallelogram.
Writes that, as opposite sides in a parallelogram are equal, OA = BC and OC = AB.
Also, as opposite angles in a parallelogram are equal, ∠AOC = ∠ABC =
90°
(Award full marks if students first proves that OABC is a rectangle using angle sum property and then shows that the adjacent sides are equal.)
Concludes that OABC is a square as all of its angles are 90°, and OA = AB = BC = OC.
Q30. Shown below is a semicircle of radius 1 unit….
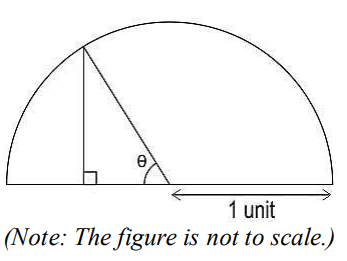
Make necessary constructions and show that:
tan θ/2 = sinθ/1+cosθ
Answer. Draws a rough figure with the necessary constructions. The figure may look as follows:

Writes that in ΔRPO,
sin θ = 𝑅𝑃
𝑂𝑅
=> RP = sin θ
Writes that in ΔRPO,
cos θ = 𝑃𝑂
𝑂𝑅
=> PO = cos θ
Writes that in ΔRPQ,
tan θ/2 = RP/PQ
⇒ tan θ/2 = sinθ/1+cosθ
Q31. Naima is playing a game and has two identical 6-sided dice. The faces of the dice have 3 even numbers and 3 odd numbers.
She has to roll the two dice simultaneously and has two options to choose from before rolling the dice. She wins a prize if:
Option 1: the sum of the two numbers appearing on the top of the two dice is odd.
Option 2: the product of the two numbers appearing on top of the two dice is odd.
Which option should Naima choose so that her chances of winning a prize is higher? Show your work.
Answer. Writes that the sum of the two numbers on the dice is one of these:
odd + odd = even
odd + even = odd
even + odd = odd
even + even = even
Finds the probability of getting an odd number as the sum on rolling the two dice as 1/2.
Writes that the product of the two numbers on the dice is one of these:
odd × odd = odd
odd × even = even
even × odd = even
even × even = even
Finds the probability of getting an odd number as the product on rolling the two dice as 1/4.
Hence, concludes that Naima should choose option 1.
Section D – Long Answer Type Questions
Q32. Manu and Aiza are competing in a 60 km cycling race. Aiza’s average speed is 10 km/hr greater than Manu’s average speed and she finished the race in hours less than Manu.
Find the time taken by Manu to finish the race. Show your work.
Answer. Assumes the time Manu took to finish the race as t hours and writes the equation for his average speed as 60/𝑡 km/hr.
Frames the equation for Aiza using the given information as:
(60/𝑡 + 10)(t -1/2) = 60
Simplifies the above equation into standard quadratic equation form as:
2t/2 – t – 6 = 0
Factorises the above equation as (t – 2)(t + 3/2) = 0
Finds the time taken by Manu to finish the race as 2 hours.
OR
Q32. Shown below is a cuboid with water in two different orientations. The length, breadth and height of the cuboid are distinct. The cuboid has 480 cm³ of water….
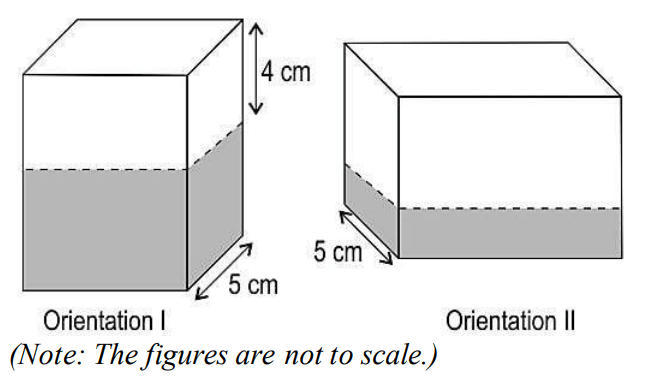
If the height of water in orientation II is half of that in orientation I, then find the heights of water in both orientations. Show your work.
Answer. Assumes the vertical length of the cuboid in orientation I as h cm and finds
the height of water as (h – 4) cm.
Finds the height of water in orientation II as 1/2(h – 4) cm.
Writes the equation for the volume of water as:
5 × h × 1/2(h – 4) = 480
Simplifies the above equation as:
h² – 4h – 192 = 0
Solves and finds the roots of the above equation as (-12) and 16.
(Rejects h = (-12) as height cannot be negative.)
Finds the height of water in:
orientation I as 16 – 4 = 12 cm
orientation II as 1/2× 12 = 6 cm
(Award full marks if an alternate method is correctly used.)
Q33. In the following figure, ΔABC is a right-angled triangle, such that:
♦ AC = 25 cm
♦ PT || AB and SR || BC…
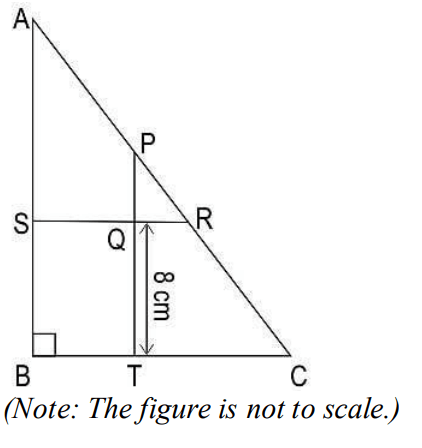
Find the area of ΔPQR. Show your work.
Answer. Finds PR as PC – RC.
Finds RC as 50/5 = 10 cm and PC as 50³cm.
Hence, finds PR as 20³cm.
Writes that ΔPQR ∼ ΔPTC by basic proportionality theorem, as QR || BC.
Writes that 𝑃𝑅/𝐶𝑅 = 𝑃𝑄/𝑄𝑇.
Hence, 20/10×3 = 𝑃𝑄/8
=> PQ = 16³cm.
Uses Pythagoras theorem in ΔPQR to find the length of QR as:
QR = (√20/3)² – (√16/3)² = 4 cm
Finds the area of ΔPQR as 1/2 × 4 × 16/3 = 32/3cm².
(Award full marks if a different solution method is used correctly to find the answer.)
Q34. Two rectangular sheets of dimensions 45 cm × 155 cm are folded to make hollow right circular cylindrical pipes, such that there is exactly 1 cm of overlap when sticking the ends of the sheet. Sheet 1 is folded along its length, while Sheet 2 is folded along its width. That is, the top edge of the sheet is joined with its bottom edge in both the sheets, as depicted by the arrow in the figure below. Both pipes are closed on both ends to form cylinders….
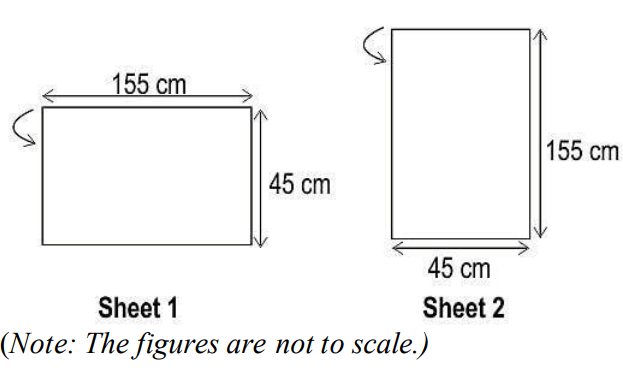
i) Find the difference in the curved surface areas of the two cylinders.
ii) Find the ratio of the volumes of the two cylinders formed.
Show your work.
(Note: Use π as 22/7. Assume that the sheets have negligible thickness.)
Answer. i) Writes that, in the sheet 1 cylinder, the height of the cylinder = 155 cm.
Hence finds the area wasted in overlap = 155 x 1 = 155 cm².
Write that, in the sheet 2 cylinder, the height of the cylinder = 45 cm.
Hence finds area wasted in overlap = 45 x 1 = 45 cm².
Writes that, as the sheets used are identical, the difference in curved
surface area = difference between area wasted in overlap = 155 – 45 = 110 cm².
(Award full marks if solved using formula).
ii) Notes that the circumference of the circle in the Sheet 1 cylinder is:
45 cm – 1 cm = 44 cm
Finds the radius of the sheet 1 cylinder as 7 cm.
The working may look as follows:
2πr1= 44 cm
=> r1 = 7 cm
Notes that the circumference of the circle in the Sheet 2 cylinder is:
155 cm – 1 cm = 154 cm
Finds the radius of the sheet 2 cylinder as 49/2cm.
The working may look as follows:
2πr2 = 154 cm
=> r2 = 49/2cm
Finds the ratio of the volumes of the two cylinders as follows:…
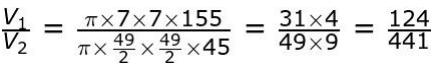
where V1 is the volume of the cylinder made by sheet 1, and V2 is the volume of the cylinder made by sheet 2.
OR
Q34. Shown below is a cylindrical can placed in a cubical container….
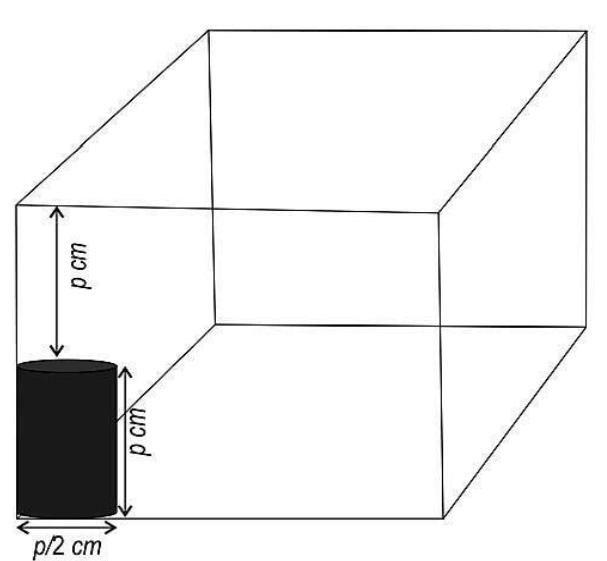
i) How many of these cans can be packed in the container such that no more cans are fitted?
ii) If the capacity of one can is 539 ml, find the internal volume of the cubical container.
Show your work.
(Note: Take π as 22/7.)
Answer. i) Find the side of the cubical container as 2p from the figure.
Calculates that 2p ÷ 𝑝/2 = 4 cans can be packed in each of the length’s and the breadth’s directions in the container.
Finds the total number of cans that can fit in the container as:
4 × 4 × 2 = 32
ii) Writes the formula for the volume of the can to find the value of p as:
539 = 22/7 × p²/16 × p
Solves the above equation to find the value of p as 14 cm.
(Award 0.5 marks if only the formula for the volume of a cylinder is written correctly.)
Find the side of the cube as 2 × 14 = 28 cm.
Find the internal volume of the cubical container as (28)³ cm³ or 21952 cm³.
Q35. A car assembly unit assembles a limited number of cars daily, depending on the prevailing demand. The following table presents an analysis of the number of cars assembled by the unit over three consecutive months:
. Cars Assembled Per Day Number of Days
0 – 4 33
4 – 8 18
8 – 12 21
12 – 16 11
16 – 20 7…
i) If the demand for the cars is doubled, estimate how many cars on average should be assembled per day such that the increased demand is met.
ii) At least on how many days, less than the average number of cars were assembled?
Show your work.
Answer. i) Prepare the frequency distribution table as below:…
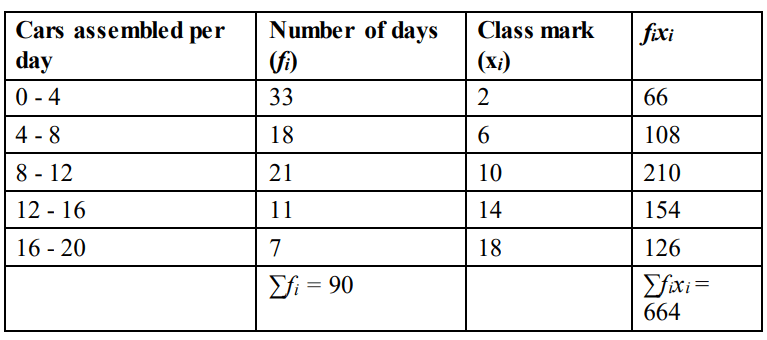
Finds the mean of the given data as 664/90 = 7.38 approximately.
(Award 0.5 marks if only the formula for mean is written correctly.)
As the demand has doubled, the new average to meet the demand should be:
2 × 7.38 = 14.76 approximately.
Concludes that nearly 15 cars should be assembled per day on average to meet the increased demand.
ii) From the table concludes that as the mean lies in the range of (4 – 8), at least 33 days less than the average number of cars were assembled.
Section E – Case Study Question
Q36. Answer the questions based on the given information.
An interior designer, Sana, hired two painters, Manan and Bhima to make paintings for her buildings. Both painters were asked to make 50 different paintings each.
The prices quoted by both the painters are given below:
♦ Manan asked for Rs 6000 for the first painting, and an increment of Rs 200 for each following painting.
♦ Bhima asked for Rs 4000 for the first painting, and an increment of Rs 400 for each following painting.
(i) How much money did Manan get for his 25th painting? Show your work.
(ii) How much money did Bhima get in all? Show your work.
(iii) If both Manan and Bhima make paintings at the same pace, find the first painting for which Bhima will get more money than Manan. Show your steps.
OR
(iii) Sana’s friend, Aarti hired Manan and Bhima to make paintings for her at the same rates as for Sana. Aarti had both painters make the same number of paintings and paid them the exact same amount in total.
How many paintings did Aarti get each painter to make? Show your work.
Answer. i) Notes that the amounts Manan is paid for each painting form an AP.
Takes a = 6000, d = 200 and n = 25 to find the amount as 6000 + (25 – 1)200 = Rs 10800.
ii) Finds the total amount earned by Bhima as follows:
S50 =50/2 [2(4000) + (50 – 1)(400)]
Solves the above expression to find the total amount as Rs 6,90,000.
iii) Frames equation as follows:
6000 + (n – 1)200 = 4000 + (n – 1)400
Solves the above equation to find the value of n as 11.
Writes that, since they both earn the same amount for the 11th painting, as Bhima’s increment is more, Bhima gets more money than Manan for the 12th painting.
OR
iii) Assumes that the number of paintings required is n.
Frames equation as follows:
Sn(Manan) = Sn(Bhima)
=> 𝑛/2 [2(6000) + (n -1)200] = 𝑛/2 [2(4000) + (n -1)400]
Solves the equation from step 1 to find n as 21.
Q37. Answer the questions based on the given information.
In the game of archery, a bow is used to shoot arrows at a target board. The player stands far away from the board and aims the arrow so that it hits the board.
One such board, which is divided into 4 concentric circular sections, is drawn on a coordinate grid as shown. Each section carries different points as shown in the figure. If an arrow lands on the boundary, the inner section points are awarded….
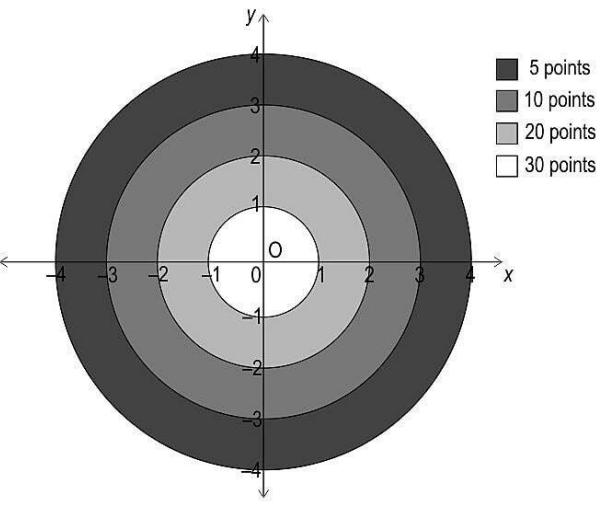
(i) After shooting two arrows, Rohan scored 25 points.
Write one set of coordinates for each arrow that landed on the target.
(ii) If one player’s arrow lands on (2, 2.5), how many points will be awarded to the player? Show your work.
(iii) One of Rohan’s arrow landed on (1.2, 1.6). He wants his second arrow to land on the line joining the origin and first arrow such that he gets 10 points for it.
Find one possible pair of coordinates of the second arrow’s landing mark.
Show your work.
OR
(iii) An arrow landed on the boundary and is worth 20 points. The coordinates of the landing mark were of the form (m, -m). Find all such coordinates. Show your steps.
Answer. i) Writes two pairs of possible coordinates such that Rohan scored 20 and 5 points for them. For example, (1.5, 0) and (3.5, 0).
ii) Finds the distance of (2, 2.5) from (0, 0) as:
√(4 + 6.25) = √10.25 units
Hence, concludes that 5 points will be awarded.
(Award full marks if students answer correctly based on any other method with appropriate justification.)
iii). Finds the distance of (1.2, 1.6) from the origin as:
√{(1.2)2 + (1.6)2} = 2 units
Assumes that the second arrow lands on the boundary mark and writes that the ratio in which the first arrow divides the origin and the second arrow’s landing mark is the ratio of their radii = 2:1.
Assumes the coordinates of the second arrow’s landing mark as (x, y) and uses section formula to write:
(2𝑥+0/3, 2𝑦+0/3) = (1.2, 1.6)
Solves the above equation to find the values of the coordinates of the second arrow’s landing mark as (1.8, 2.4).
OR
iii) Identifies the distance between the origin and the coordinate (m, -m) as 2 units and uses the distance formula to write the equation as:
m² + (-m)² = 2²
Simplifies the above equation as 2m² = 4.
Solves the above equation to get y as √2 and (-√2).
Finds the coordinates as (√2, -√2) and (-√2, √2).
Q38. Answer the questions based on the given information.
A drone is an aircraft without any human pilot and is controlled by a remote control device. Its various applications include policing, surveillance, photography, precision agriculture, forest fire monitoring, river monitoring, and so on.
David used an advanced drone with a high-resolution camera during an expedition in a forest region that could fly up to 100 m height above ground level. David rode on an open jeep to go deeper into the forest. The initial position of the drone with respect to the open jeep on which David was riding is shown below….
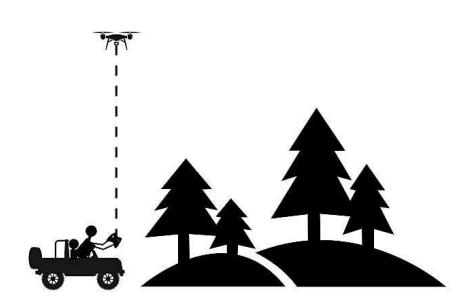
David’s jeep started moving to enter the forest at an average speed of 10 m/s. He Simultaneously started flying the drone in the same direction as that of the jeep.
(i) David reached near one of the tallest trees in the forest. He stopped the drone at a horizontal distance of 5√3 m from the top of the tree and at a vertical distance of 65 m below its maximum vertical range….
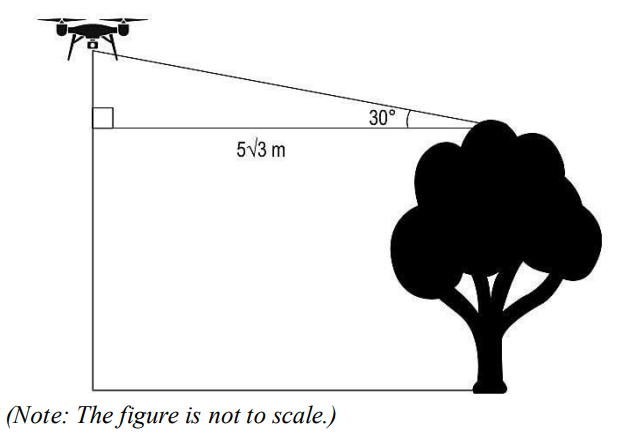
If the angle of elevation of the drone from the top of the tree was 30°, find the height of the tree. Show your work.
(ii) The drone was flying at a height of 30√3 meters at a constant speed in the horizontal direction when it spotted a zebra near a pond, right below the drone.
The drone traveled for 30 meters from there and it could see the zebra, at the same place, at an angle of depression of θ from it.
Draw a diagram to represent this situation and find θ. Show your work.
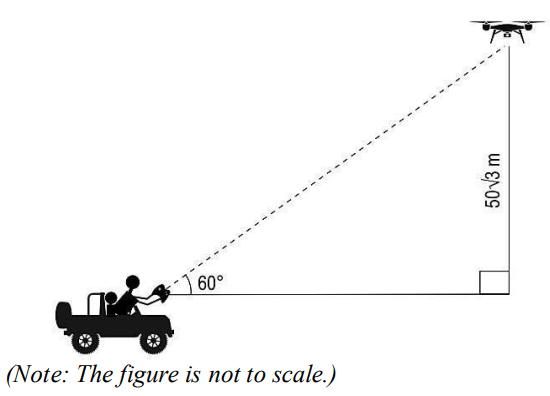
(iii) After 2 minutes of starting the expedition both the drone and the jeep stopped at the same moment so that the drone can capture some images. The position of the drone and the jeep when they stopped is as shown below.
… 
iii) At some point during the expedition, David kept the drone stationary for some time to capture the images of a tiger. The angle of depression from the drone to the tiger changed from 30° to 45° in 3 seconds as shown below.
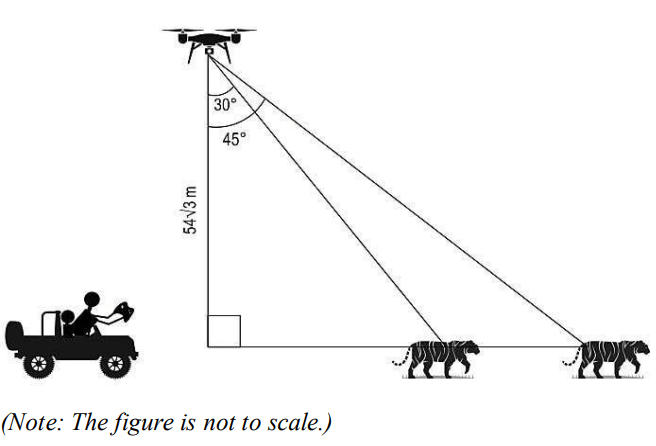
What was the average speed of the tiger during that time? Show your work.
(Note: Take √3 as 1.73.)
Answer. i) Assumes the vertical distance between the top of the tree and the drone to
be h and finds h as:
h = 5√3 × tan 30° = 5√3 × 1/√3 = 5 m
Finds the height of the tree as 100 – 65 – 5 = 30 m.
ii) Draws a rough diagram to represent the situation. The figure may look as follows:…
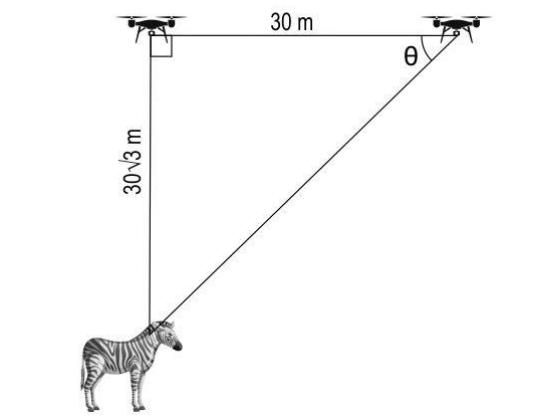
Finds the value of θ as:
tan θ = 30√3/30 = √3
Thus finds the value of θ as 60°.
iii) Assumes the horizontal distance between the remote and the drone as x and finds its value as:
x = 50√3/tan 60° = 50 m
Find the distance covered by the jeep in 2 minutes as:
10 × 120 = 1200 m
Finds the horizontal distance covered by the drone before it stopped as:
1200 + 50 = 1250 m
Finds the speed of the drone as:
1250/120 = 10.42 m/s
OR
iii) Assumes the horizontal distance between the drone and the tiger to be x when the angle of depression was 30° and finds the value of x as:
x = 54√3 × tan 30° = 54√3 × 1/√3 = 54 m
Assumes the horizontal distance between the drone and the tiger after 3 seconds as y and finds the value of y as:
y = 54√3 × tan 45° = 54√3 m
Finds the distance covered by the tiger in 3 seconds as:
54√3 – 54 = 39.42 m
Finds the average speed of the tiger during that time as:
39.42/3 = 13.14 m/s….
error: Content is protected !!